Aim
This physics investigation aims to examine the effect of temperature change on the spring constant of a metallic steel spring.
Introduction
This investigation is linked to my long interest in and participation in Bungee jumping. In this game, I am particularly interested in how people are able to jump from great heights on elastic cords. This investigation is linked to my long interest in and participation in Bungee jumping. In this game, I am particularly interested in how people are able to jump from great heights on elastic cords. I realized that a person’s weight on the spring is similar to a mass hanging on a spring, and the extension of this spring could be a subject weight or force that acts on it.
The spring constant is the force ratio of a spring to its displacement (Dwivedi 1). The spring constant is calculated through the following general formula;
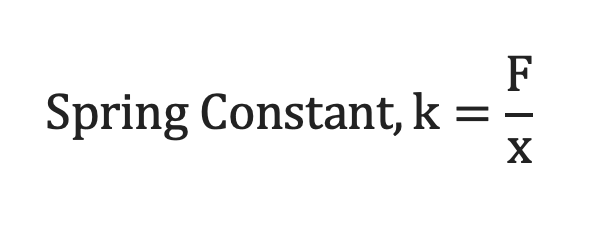
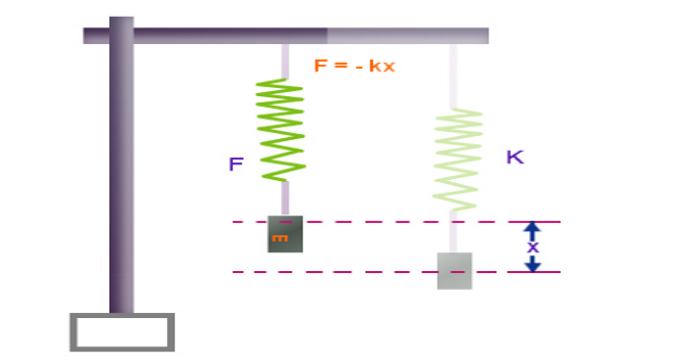
Different factors could influence the constant of the spring represented in Figure 1 above. According to Garrett (2), the spring’s length, geometry, and material properties could directly influence the spring constant. Additionally, temperature could affect the spring constant due to changes in thermal expansion when the spring is heated or cooled. The interest of this investigation is to increase the temperature and examine the impact of this increase on the spring constant of a steel spring while controlling the spring’s length, geometry, and material properties.
Hypothesis
It is hypothesized that the spring constant of the steel spring will decrease with an increase in temperature. This hypothesis is supported by the study of Werner et al. (2), which supposes that when the temperature in an elastic body is increased, the metallic lattice’s atoms tend to vibrate with increased energy, making the atoms occupy more space. As a result, the spring’s length increase, leading to a reduction of stiffness.
Variables
Independent Variable
The Independent variable in this scientific investigation is temperature. The temperature will be varied from 250C to 500C increments of 50C using the hot water and measured by mercury thermometer (± 0.10C).
Dependent Variable
The spring constant of the steel spring will be the dependent variable. The calculation of this variable will be based on the mass of a 100 g mass and the change in the length of the spring.
Control Variable
The major control variables in this scientific investigation are presented in table 1.
Table 1: Main Control Variables, their Impact, and Control Mechanism
| Control Variable | Impact of the Variable | Mechanism of the Control |
| Mass | The size of the mass attached to the steel spring will directly affect the extension. Thus, the use of different masses will lead to inconsistent extensions across the trials. | One 100 g mass will be used in all the trials. |
| Steel spring | Variations of springs will vary the spring constants since different springs could have different properties. | A single spring will be used across all the trials of this investigation. |
| Experimental technique | Changing the techniques of conducting the experiment could lead to inconsistent results; for instance, heating the spring while hanging on the clamp stand in some steps and heating the spring in water before suspending on the spring. | A unified technique for performing the experiment will be ensured and maintained across all the trials. |
| Environmental temperature | Fluctuations in environmental temperature can lead to compressions and tensions of the spring leading to inconsistent extensions across the trials. | The entire experiment will be conducted in a single room to ensure maximum control in environmental temperature conditions. |
Apparatus
- A stopwatch
- A clamp stand
- An electronic beam balance
- A steel spring
- A wire to suspend the spring
- A meter ruler
- A 100 g mass
- A hot plate
- A beaker
- Distilled water
- A mercury thermometer
Method
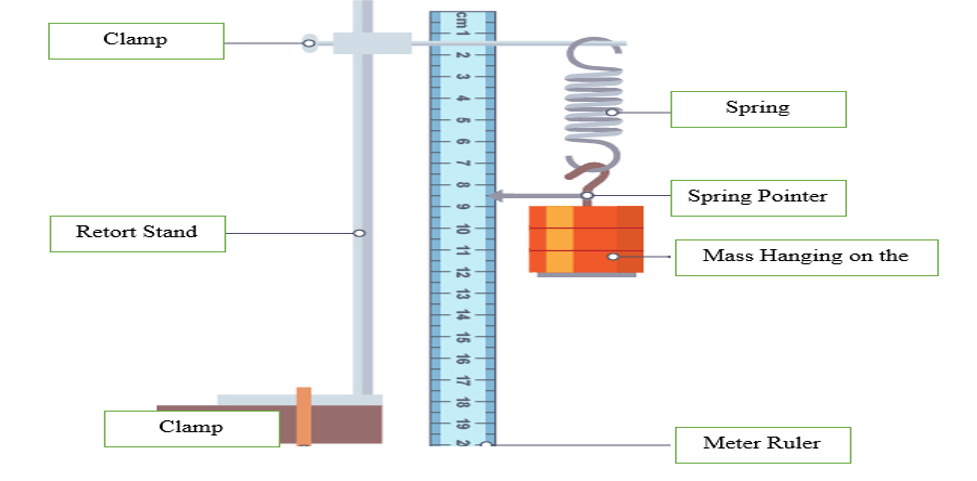
- The spring was then suspended vertically on the clamp stand, as depicted in Figure 1, ensuring that it did not touch any surface.
- The 100 g mass was then placed onto the lower part of the spring, and its initial extension was measured using the ruler.
- The steel spring was then placed into the water, placed in a beaker, and heated on a hot plate to a temperature of 250C with the help of the mercury thermometer.
- The spring was then suspended on the clamp stand as in step 1, and the extension of the spring was measured.
- Steps 3-4 were repeated for four more trials.
- Steps 3-5 were repeated at temperatures of 300C, 350C, 400C, 450C, and 500C, recording the results for each trial in the raw data table.
Set-up
Risk Assessment
- The steel spring and the rest of the equipment were handled with prime care to prevent unprecedented injuries or damages.
- The hot steel spring and beaker were handled with pliers and a beaker holder to prevent accidental burns.
- Protective gear, including safety goggles and hand gloves, was worn during the entire experiment to reduce the chances of injuries.
Raw Data
Initial extension of the spring, e1 = 3.9 cm
Table 2: Extension of the Metallic Steel Spring at different Temperatures
| Temperature, T | Extension of the Metallic Steel Spring, e2 | ||||
| Trial 1 | Trial 2 | Trial 3 | Trial 4 | Trial 5 | |
| 50.0 | 5.5 | 5.4 | 5.4 | 5.3 | 5.5 |
| 45.0 | 5.3 | 5.2 | 5.1 | 5.2 | 5.3 |
| 40.0 | 5.0 | 5.1 | 5.0 | 4.9 | 5.2 |
| 35.0 | 4.7 | 4.8 | 4.7 | 4.6 | 4.7 |
| 30.0 | 4.5 | 4.6 | 4.5 | 4.7 | 4.5 |
| 25.0 | 4.0 | 4.2 | 4.1 | 4.2 | 4.1 |
Data Processing
Calculations of Change in Length, x
The change in length of the steel spring corresponding to the various conditions of temperature was first determined as the difference between the initial and final extensions of the spring when loaded by the 100 g mass.

The measurement corresponding to the first trial of 50.00C was used in a sample calculation;
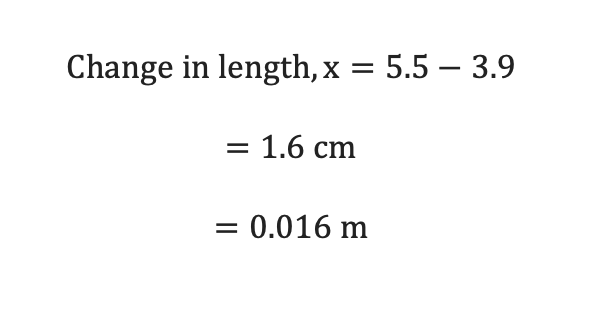
Table 3: Change in Lengths of the spring at different Temperatures
| Temperature, T | Change in lengths of the Metallic Steel Spring, x | ||||
| Trial 1 | Trial 2 | Trial 3 | Trial 4 | Trial 5 | |
| 50.0 | 0.016 | 0.015 | 0.015 | 0.014 | 0.016 |
| 45.0 | 0.014 | 0.013 | 0.012 | 0.013 | 0.014 |
| 40.0 | 0.011 | 0.012 | 0.011 | 0.01 | 0.013 |
| 35.0 | 0.008 | 0.009 | 0.008 | 0.007 | 0.008 |
| 30.0 | 0.006 | 0.007 | 0.006 | 0.008 | 0.006 |
| 25.0 | 0.001 | 0.003 | 0.002 | 0.003 | 0.002 |
Calculations of Average Change in Lengths and Corresponding Uncertainty
The average change in length at the different temperatures and the corresponding uncertainties were then calculated using the following general formulas;

Table 4: Average Change in Lengths and Corresponding Uncertainty at Different Temperatures
| Temperature, T | Average Change in Length, (m) | Uncertainty, |
| 50.0 | 0.0152 | 0.0010 |
| 45.0 | 0.0132 | 0.0010 |
| 40.0 | 0.0114 | 0.0015 |
| 35.0 | 0.0080 | 0.0010 |
| 30.0 | 0.0066 | 0.0010 |
| 25.0 | 0.0022 | 0.0010 |
Determination of Spring Constant, k
The spring constant was calculated as a function of force due to the mass suspended onto the spring and the average change in length;

The corresponding uncertainty of the spring constant was then calculated as a function of the uncertainty of the mass and the uncertainty of the change in length of the steel spring;
Table 5: Spring Constant of the Steel Spring and Uncertainties at Different Temperatures
| Temperature, T | Spring Constant of the Steel Spring, k (N/m) | Uncertainty, ∆k (N/m) |
| 50.0 | 64.54 | 0.067 |
| 45.0 | 74.32 | 0.077 |
| 40.0 | 86.05 | 0.133 |
| 35.0 | 122.63 | 0.126 |
| 30.0 | 148.64 | 0.153 |
| 25.0 | 445.91 | 0.456 |
Graph of Spring Constant against Temperature
The data in table 4 was used to create a linear graphical plot of spring constant against the temperature. The uncertainties of the spring constant were used on the linear plot as the error bars. This graph was created in Microsoft Excel.
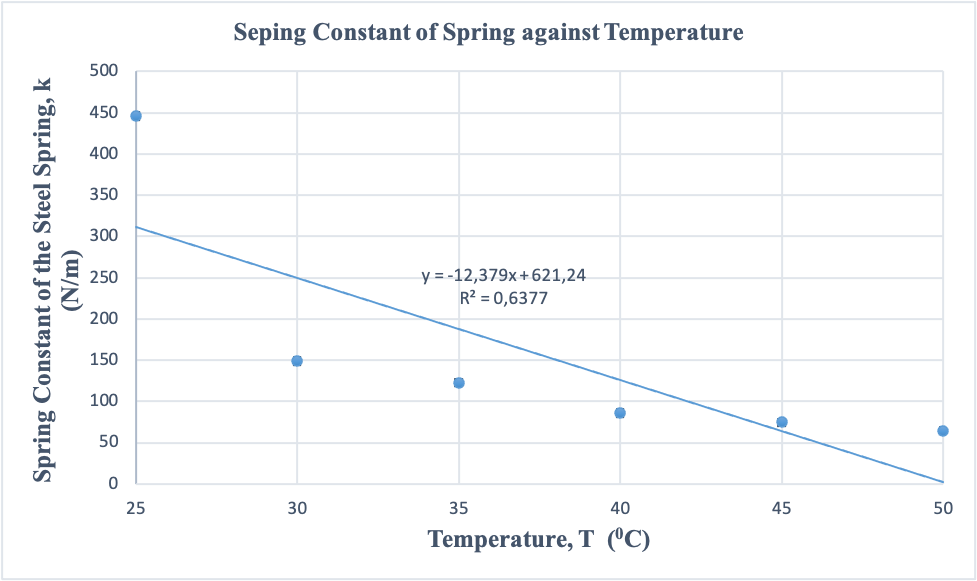
The linear graph in Figure 3 above shows a downward trend in the spring constant of the steel spring as the temperature is increased, defined by a slope of -12.379. The square regression constant (0.6377) was greater than 0.5, indicative a strong negative relationship between the spring constant and temperature. Additionally, the error bars on the linear plot were very small in size, indicative of high reliability and accuracy both in the method used and results collected and processed in this scientific investigation.
Conclusion
This investigation was purposed to examine the effect of temperature change on the spring constant of a metallic steel spring. It had been hypothesized that the spring constant of the steel spring would decrease. A lab-based investigation was designed using a single steel spring, heated at different temperatures, hanged on a clamp stand, and loaded with a 100 g mass. The resulting changes in the lengths of the springs were used to calculate the spring constants at different temperatures. The processed results revealed that spring constants of the steel spring decrease with a rise in temperature. Ideally, the spring constant was 445.91 N/m at 25°C and 64.54 N/m at a temperature of 50°C. The decrease in spring constant on increasing temperature was associated with thermal expansion as the temperature increased. The thermal expansion weakened the atomic bonds of the spring, making the atoms occupy more space and increasing cross-sectional area, which reduced the spring’s stiffness, hence the reduction in spring constant. The investigation provided a better understanding of the basic relationship between temperature changes and a metallic spring’s spring constant. These results could be used in different fields, including the design of mechanical devices that are temperature sensitive.
Evaluation
The experiment of this investigation was performed under several controlled conditions, a factor that favored increased the accuracy of final results. Additionally, experimental data of extensions of the spring were collected at five different temperatures providing a comprehensive and valid evaluation of the effect of temperature on the spring constant. However, there were some limitations, which may have affected the results, as depicted below.
Table 6: Main Limitations, their Impact, and Proposed Improvements
| Limitation | Significance | Proposed Improvement |
| Systematic errors | The apparatus used to measure the length of the spring had a high uncertainty, leading to possible measurement errors. | Apparatus with higher precision could be used, such as the vernier callipers in place of the meter ruler, for more accurate results. |
| Limitation of type of spring | Only one type of metallic steel spring was used, limiting the validity of the investigation. | The experimental process could be repeated with different types of steel springs for a more comprehensive and valid investigation. |
Proposed Extension
This scientific investigation could be extended further in different ways. For instance, the experimental process could be repeated with a higher range of temperatures to find out whether there exists any threshold beyond which an increase in temperature will not reduce the spring constant’s magnitude. In addition, the effect of temperature on the spring constant could be evaluated with other types of springs, such as rubber springs.
Works Cited
Dwivedi, Kamal. Spring Constant: Definition, Formula, Unit, Calculation. 7 Jan. 2023, www.mechical.com/2022/07/spring-constant.html.
Garrett, Steven L. “Elasticity of Solids.” Understanding Acoustics, 2020, pp. 179–233, https://doi.org/10.1007/978-3-030-44787-8_4.
Werner, Brian T., Bonnie R. Antoun, and George B. Sartor. “Thermal Degradation of Extension Springs.” Challenges in Mechanics of Time-Dependent Materials, Volume 2: Proceedings of the 2015 Annual Conference on Experimental and Applied Mechanics. Springer International Publishing, 2016.
 write
write