Comprehending mathematical concepts is demonstrated by how they relate to other things. Most students see the concepts as separate ideas rather than as parts of a whole. This may cause major mathematical problems. I will concentrate on the concept of polynomials in this presentation. Algebra 1 covers the concepts of polynomials, equations, inequalities, solutions, exponents, and graphs. Monomials, polynomial operations and degrees, factoring polynomials, roots and graphs of polynomials are all polynomial sub-concepts. They necessitate a basic understanding of Cartesian planes, number lines, the real number system, and key terms such as constants and variables. Functions, linear equations and inequalities, and the system of two linear equations all require graphing. Algebra 1 also helps students understand the laws of exponents, which are useful in square roots and scientific notation.
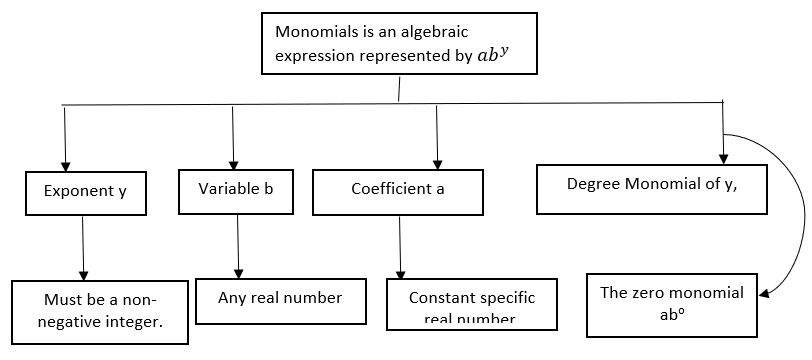
A polynomial is a mathematical expression made up of coefficients and variables. As the name implies, poly means many and nominal indicates terms, so a polynomial is a term with many terms. Polynomials are typically defined as the sum or difference of variables and exponentials. 3x2 + 4x – 6 is an example of a polynomial. A monomial is an exponential function that is comprised of only one term. The algebraic expression is only known as a monomial if the single term is a non-zero designation. When two or more monomial terms are added together, they form polynomials. Constant coefficients, exponents, variables, and degrees are used to describe monomials. For example, a monomial can be written as: aby where ay is the constant coefficient, b is the variable, and y is a non-negative integer known as an exponent; aby, is just a representation, and any letter can be used to represent the constant and variables. Evaluating monomials is straightforward; for example, if our variable b=4, constant a = 5, and y = 3, then 5 x 43 = 320. Because a and y are constants, replacing the variable x produces results for aby,
Importance of Algebraic Concept for Pre-Service Teachers in the Development of Mathematical Knowledge.
New teachers must have educational experience targeted at specific aspects of algebra in preservice teacher development so that, in their teaching, they can enhance it in their pupils (Magiera, et al., 2011). Mathematical expertise and instruction are both included in the identity formation. Mathematics knowledge entails understanding how to use mathematics as well as knowing its interpretations and principles. The teacher must understand and apply procedures, as well as why these procedures work. According to NCTM (2000), educators must be well-versed in and fully comprehend the mathematics they are teaching. Additionally, according to Ponte and Chapman (2008), preservice teacher training faces the problem of integrating curriculum and instruction, as well as instructing preservice teachers in the same manner that they are anticipated to educate their learners. As a result, they must be familiar with algebra and what it entails in primary school in order to utilize it later in their profession, creating learning scenarios to improve their students’ algebraic reasoning.
Pre-service teachers completing an undergraduate education course at Australia’s University of Notre Dame, for example, can take a unit on Early Mathematical Learning for Young Students. Students enrolled in the program can apply the unit toward a specialty or major in mathematics instruction. The unit lasts about fifteen weeks and requires 40 hours of specialized classroom instruction. The Australian Association of Mathematics Teachers emphasized the significance of teachers’ mathematical content knowledge, saying: “Excellent instructors have a solid, coherent understanding of the mathematics relevant to the student level they instruct.”
Early algebra advocates incorporating algebra into primary education beginning in the first years of education. The success of this integration is heavily reliant on teacher training. Pre-service teaching is the first step in developing capable teachers for all students. Due to time constraints, most students are taught simple methods for arriving at algebraic solutions. Simple mathematical techniques do not improve mastery of major concepts, resulting in a lack of foundational knowledge. Creating concept maps assists pre-service teachers in identifying the central ideas of algebra, as well as equipment and approaches for perfecting these concepts. It gives them the idea that students learn differently and attain different goals. There are various approaches to comprehending algebraic concepts. Methods and strategies that actively engage students and match their abilities should be used.
Concept map on Monomials
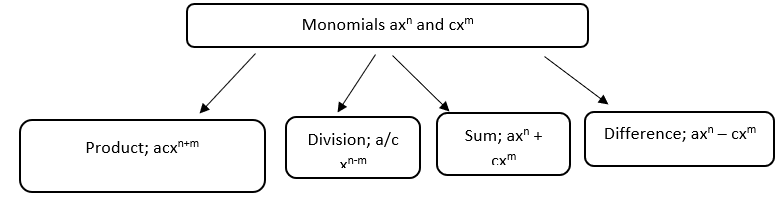
Operations on monomials.
Monomials are subjects to addition, subtraction, multiplication and division. Monomials are closed under addition, subtraction, multiplication and division (Cladwell, 2009).
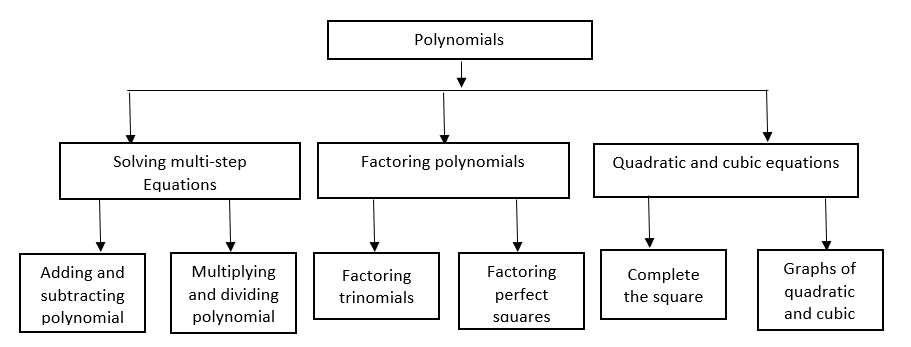
When two or more monomials are added together, polynomials are formed. Terms are monomials that make up a polynomial. 5×4 + 3×3 has two terms, for example. If the monomials have distinct degrees and are arranged in either ascending or descending order, the polynomial is said to be standard. They are also comparable if they contain the same set of terms, such as 3×5 + 2×6 and 2×6 + 3×5. When two polynomials are added, subtracted, multiplied, or divided, the resulting polynomial is also a polynomial (Cladwell, 2009). Polynomials can be solved to yield a real number.
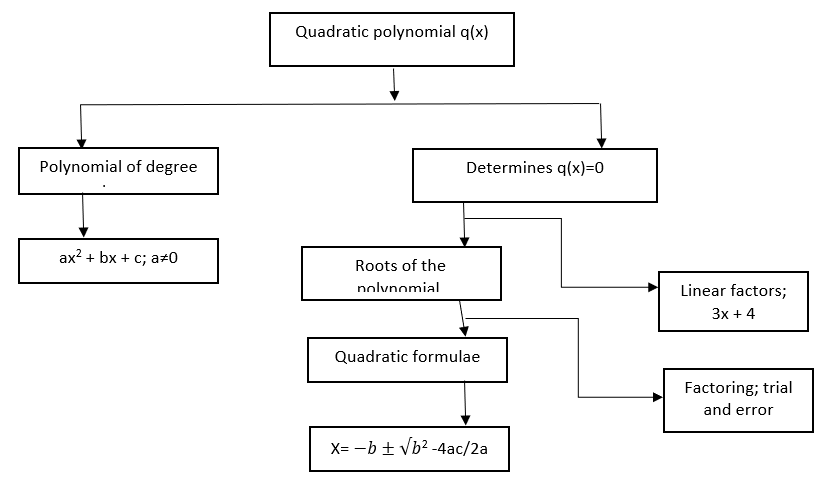
Quadratic polynomials
A quadratic polynomial is an expression that has a term of degree two. It is written as ax2 + bx + c; where a≠0.
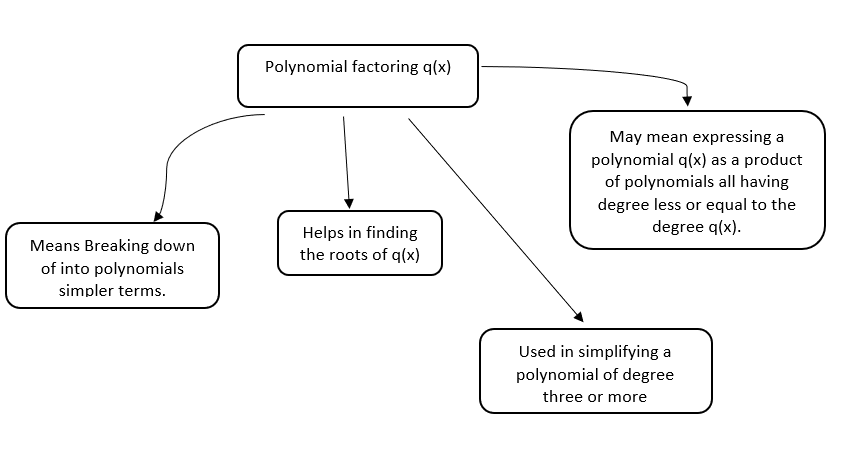
Polynomial factoring
It is described as the breakdown of polynomials into simpler terms so that when these terms are multiplied, the original polynomial is obtained. Finding the highest common factor, perfect squares, and perfect cubes are all techniques for factoring polynomials. Polynomial factoring can produce completely factored forms that are products of the original polynomials (Cladwell, 2009).
Learning outcomes
By the end of the topic, students are supposed to:
- Evaluate and solve algebraic equations.
- Utilize the three laws (associative, commutative and distributive) to come up with expressions.
- Use substitution to answer a set of linear equations
- Identify the degree, coefficients and terms in a polynomial.
- Understand and use exponents correctly.
- Determine popular monomial factors of polynomials
Challenges
Algebra entails comprehending symbols and expressions as well as solving expressions to obtain real-world solutions. Most students fail to understand the concept because of a lack of prerequisite knowledge from lower levels. They also lack the ability to solve and deal with linear equations. Teachers may also employ ineffective teaching methods, making it difficult for students to comprehend. Learners’ errors in addressing algebraic problems are indications of their difficulties with the material. It demonstrates that difficulty is the root cause of error. Despite the numerous efforts made by teachers, students continue to experience learning difficulties. According to Cooney, learners’ difficulties in learning mathematics should be focused on two important types of mathematical knowledge: understanding of concepts and principles (Novferma, 2016). Thus, students’ learning difficulties in studying algebra can be examined based on their knowledge of algebra ideas and concepts.
Target Group
Year 8 allows for a thorough understanding of knowledge and skills in eight areas of study, including English, science, mathematics, humanities and social science, health and physical education, and art and design. Year 8 mathematics, according to the Australian Curriculum, Assessment and Reporting Authority (ACARA), entails competency in thinking, problem-solving, fluency, and comprehension. It focuses on number and algebra, as well as other topics.
The Mathematics curriculum builds on previous concepts to solve non-routine mathematical problems and develop more abstract and logical ideas. In order to solve economic and social problems, the curriculum connects mathematical concepts with real-life situations. It also lays the groundwork for future studies by introducing geometry to students. Students will be more mathematically enriched by the end of year 8, allowing them to tackle practical examples.
Lesson Plan
| Teacher | Class: Year 10 |
| Date: 3/28/2022 | Time: 10 total instructional hours |
| Lesson Heading/Topic: Algebra 1 | |
| Lesson Objectives: Students should be able to define constant coefficients, variables, and exponents by the end of the lesson. They will also define monomials, polynomials, polynomial degrees, polynomial factoring, and what makes up a polynomial. They will find real-number solutions to polynomials. In addition, the learner should be able to use perfect squares and the difference of squares to simplify polynomials. They should also develop techniques for factoring polynomials, such as finding the greatest common factor, and solving polynomials. | |
| Key Concepts/Ideas: Number and algebra: rational and irrational numbers, logarithms and functional indices. Patterns and Algebra: Concepts on polynomial, factor and remainder theorem. Linear and non-linear relationships: exponential equations | |
| Curriculum/Syllabus Link: https://www.australiancurriculum.edu.au/f-10-curriculum/mathematics/?year=11759&year=11761&strand=Number+and+Algebra&strand=Measurement+and+Geometry&strand=Stati stics+and+Probability&capability=ignore&capability=Literacy&capability=Numeracy&capability= Information+and+Communication+Technology+%28ICT%29+Capability&capability=Critical+and+Creative+Thinking& amp;capability=Personal+and+Social+Capability&capability=Ethical+Understanding&capability =Intercultural+Understanding&priority=ignore&priority=Aboriginal+and+Torres+Strait+Islander +Histories+and+Cultures&priority=Asia+and+Australia%E2%80%99s+Engagement+with+Asia&priority= Sustainability&elaborations=true&elaborations=false&scotterms=false&isFirstPageLoad=false |
|
| Skills: Comprehension, Fluency, Problem-solving, Rationalization. | |
| Values And Attitudes
|
|
| TIME | TEACHER ACTION | STUDENT-CENTRED ACTIVITIES (including assessment of learning) |
RESOURCES |
| Introduction | Angle 1: Use earlier solved polynomials and other algebraic questions to assist students in employing algebraic approaches and rationale. By evaluating solved questions, students will develop a greater understanding of the logic used to answer algebraic equations.
Angle 2: Educate students on adequate utilization of the structure of algebraic representations (foundational mathematical features and relationships such as presence of an inequality) |
Students describe the steps they took to find the solution and explain their rationale.
Students must also respond to specific questions about the solution strategy and whether it is reasonable and arithmetically accurate. Students make links between different problems and mathematically compatible analytical approaches by paying attention to structure. This is illustrated in the main body below A special emphasis is placed on mathematical similarities because they help to ease the solution of algebra problems. |
Course text-books, electronic material such as scholarly journals, websites and extra informational documents such as pdfs.
Face-to-face classroom discussions. |
| Main body | Contd. Angle 1: Discuss with the students the following pedagogical questions; 1) Why do the steps work in the specified order? 2) Does this step strategy always work? 3) Could the solved problem have been tackled in fewer steps or differently? 4) What major mathematical concepts connect to the solution?
Angle 2: Encourage use of language that accurately reflects mathematical validity and structure, helping students comprehend the relationships. Educate learners that various algebra representations can give varied information about a given problem |
Students participate in general classroom discussion, structured group work and on independent learning activities to sufficiently introduce, discuss about and work with solved algebraic problems
Students identify algebra problems and representations that may initially appear to be different but are mathematically similar e.g., though 2x + 6 =12 and 2((x + 1) + 6 =12 appear different, they have the same structure as 2 times a given quantity plus 6 equals 12 |
Group discussions |
| Closure | Educate students to identify and come up with solutions strategies for tackling algebra problems, Provide adequate examples that show the use of multiple solution strategies. Include standard strategies and alternative ones that may be less common. | Students identify variance of effectiveness in different solution strategies used to solve a problem and solve the specified problem in another way to come up with additional strategies. | Group work |
| Scaffolding using questions
Throughout the instruction, teachers can reframe student workarounds and answers to questions using appropriate mathematical language rather than ambiguous, non-mathematical speech. For example, the teacher should explain the phases for multiplying algebraic expressions using the distributive law, and then the students should fully understand the algebraic meaning for using the distributive law as a solution technique. |
|||
Modification with a focus on indigenous students / English learners
The Australian Curriculum takes ELL students into account when accounting for student diversity. Students learning English as a second language must learn English, gain knowledge about English, and learn through English. According to ACARA, these students require specialized assistance to learn skills and build English content, and such assistance is required as long as they adhere to the curriculum’s integrity. Effective math instruction requires a strong foundation in vocabulary. It entails not only learning math-specific phrases, but also distinguishing between the mathematical meaning of a word and other meanings of that word. This activity can be tailored to English learners by assisting them in specifically learning important mathematical vocabulary in the manner described below;
- Indicating that vocabularies can have numerous interpretations. Assisting students in understanding the various meanings of words such as quarter and how to use them accurately in an algebraic system.
- Providing visual aid such as pictorial representations and hand movements. Allow students to practice their vocabulary by allowing them to work with visual elements. If there are not sufficient items for each student, display teaching aids around the classroom, and illustrate the vocabulary in front of the pupils. Use common symbols to represent mathematical concepts. Multiplication, for instance, is represented by the sign *.
- Select new and important vocabulary to pre-teach to English learners prior to the lesson. This will assist students in determining which functions are important and how to use them.
- Asking students who are fluent in both English and their indigenous language to provide language assistance to their English-learning classmates during lessons. They will understand the concepts better in their native language.
Overall, the English language program will be developed in accordance with the conceptual lesson plan in order to account for indigenous students and enable comprehension of mathematical vocabularies. Instructions and requirements will be phrased in such a way that students understand what is expected of them. For use in tests and assessments, dictionaries will allow for different translations in different dialects.
Review on Significant Theories, Teaching Models and Issues Related to Teaching Mathematics
The review takes into account influential classroom factors that affect students’ learning opportunities and teacher effectiveness. It covers learning opportunities such as pre-service teachers’ teaching practices, students’ learning activities, engagement and environment, and response. Qualifications, professional experience, program coherence, teaching capacity, and resources are all aspects of teachers and schools. Furthermore, allocating time for mathematic learning and teaching improves quality mathematics mastery. Many factors influence adequate mathematics learning opportunities, but the most important are classroom practices and student activities. Effective teaching entails enhancing students’ independence, persistence, and self-efficacy in applying mathematical concepts, as well as understanding concepts on the learning task. It also entails instructing on cognitive processes and approaches. Effective teaching strategies necessitate well-organized teaching approaches. There are three modes of communication in the classroom: conveying information, soliciting information, and providing feedback. Effective teachers require methods for organizing information so that the lesson flows and connects to other concepts. Effective teaching frameworks that improve concept understanding must concentrate on significant challenging tasks. These tasks require students to think analytically in order to optimize their achievements and understanding of concepts. The use of concept presentations aids in the development of sophisticated mathematical thinking. Engaging students in learning necessitates a supportive environment that allows students to self-regulate. Effective teachers demonstrate characteristics such as providing feedback, challenging students, and structuring activities that increase student engagement and class management. These characteristics are subject to change and have an effect on a student’s ability to learn. Because it focuses on a specific concept, concept mapping as a model improves performance. Pre-service teachers grow professionally over time, and as a result, they can perform effectively because they encounter a variety of students in their teaching practices.
One of the difficulties that pre-service educators face when teaching mathematical concepts to Middle School students is the application of conceptual information in real classroom settings (Gan, 2013; Peercy, 2012). Gan (2013), for instance, observed that pre-service instructors expressed concerns about applying the concept learned in their college courses to classroom practice. According to Peercy (2012), pre-service teachers do not apply the theories they learn in training courses and struggle to bridge the theory-practice gap. Another issue raised by pre-service instructors is the accessibility and use of teaching aids. Objects, educationalists believe, allow learners enjoy learning, encourage them to engage, and bridge the gap between conceptual and concrete principles (Larbi & Mavis, 2016). The use of teaching aids as an instructional tool encourages students to interact with teaching in practical ways. Ulla (2016), on the other hand, stated that a lack of educational tools compelled pre-service teachers to reuse strategies and techniques, reducing their effectiveness. Learning mathematics also has a time constraint. Mathematics requires patience and should be taught in a systematic manner, alongside students’ attempts at understanding and practice. Most students fail important concepts, including Algebra, because their teachers rushed through illustrations and teaching methods, leaving gaps in concept mastery. Gaps in concept mastery make learning difficult and give students the impression that mathematics is difficult. Teachers may also use techniques that are not appropriate for the target audience. Because concept mastery varies by level, appropriate methods must be used to match the learners’ capability. Students must also devote their own time to learning mathematics and practicing on a regular basis.
Reference list
Caldwell, W. (2009). Applying Concept Mapping to Algebra I. Concept Mapping in Mathematics, 24, pp.217–234.
Schoenfeld, A.H. (1999). Models of the Teaching Process. The Journal of Mathematical Behavior, 18(3), pp.243–261.
Tekin-Sitrava, R. (2017). Middle Grade Students’ Concept Images of Algebraic Concepts. Journal of Education and Learning, 6(3), p.299.
Way, C. (2015). Australian curriculum mathematics : number and algebra. Greenwood, Western Australia: R.I.C. Publications.
www.australiancurriculum.edu.au. (n.d.). Mathematics. [online] Available at: https://www.australiancurriculum.edu.au/f-10-curriculum/mathematics/?.
 write
write