Options Evaluation in Large Classes of Rough Stochastic Volatility Models

ABSTRACT

Partial differential equations (PDEs) are mathematical models widely used in physics, engineering, and finance to describe various phenomena. However, solving PDEs is often challenging, especially when the dimensionality is high. Deep learning techniques have shown great promise in solving PDEs in recent years. This review introduced a new approach for modelling local stochastic volatility using deep probabilistic programming. It uses a deep Gaussian process prior to model the volatility surface and using the model to estimate option prices. This paper discusses several papers that use deep learning to solve different PDEs. Specifically, we review papers that deal with rough stochastic volatility models, option pricing, path-dependent PDEs, high-dimensional PDEs, and martingale functional control variates. We summarize the main contributions of each paper and discuss their potential applications and limitations.

Keywords: Deep learning, Pricing function, Stochastic model, Local volatility, Path-dependent PDEs, Option pricing, Neural Networks, BSDE.

1. INTRODUCTION

1.1 General Objective

To solve PPDEs numerically based on the discretization of the pricing function, which can then be solved using deep learning techniques. This avoids the curse of dimensionality for high-level PDEs

This review discusses several papers that use deep learning to solve different types of PDEs. Specifically, we review papers that deal with rough stochastic volatility models, option pricing, path-dependent PDEs, high-dimensional PDEs, and martingale functional control variates. We summarize the main contributions of each paper and discuss their potential applications and limitations and how they relate to our main paper (Antoine & Mugad, 2019)

Antoine & Mugad (2019) proposed a deep learning framework for solving rough stochastic volatility models and used a deep Gaussian process prior to model the volatility surface and used this model to estimate option prices. According to numerical simulations, this framework provides a better alternative to the Monte Carlo simulations. The authors introduce a new approach for modelling local stochastic volatility using deep probabilistic programming.

Background

In recent years, there has been a surge of interest in using deep learning to solve PDEs. The main advantage of deep learning techniques is that they can learn the underlying structures and patterns in the data without requiring prior knowledge of the equations. Deep learning methods can also handle high-dimensional and nonlinear problems, often challenging traditional numerical methods.

The authors of the paper under review build upon previous research in stochastic volatility modelling, deep learning, and Bayesian inference. Traditional approaches to modelling stochastic volatility, such as the Heston model (Abi, 2019) (Omar, Masaaki, & Mathieu, 2016) (Omar, Gatheral, & Mathieu, 2019) (Omar, Masaaki, & Mathieu, 2016) and the SABR model (Hagan, Kumar, Lesniewski, & Woodward, 2002), have limitations in their ability to capture complex nonlinearities and to predict price options accurately. Deep learning techniques have shown promise in improving the accuracy of option pricing by providing more accurate volatility surfaces (Han, Jentzen, & E, 2018). Bayesian inference is a powerful tool for probabilistic modelling, and deep probabilistic programming has emerged as an important area of research in recent years.

Several deep-learning architectures have been proposed for solving PDEs. One popular approach is to use neural networks to approximate the solutions of the PDEs. Neural networks can be trained using supervised learning techniques to minimize the difference between predicted and true solutions.

Basis of development of Rough local volatility

The basis for the suggested developments is to speed up the calibration process for very high-dimensional PDE via a path-dependent PDE and to propose a numerical scheme that avoids the curse of dimensionality. Consider a one-dimensional asset price process

for some Brownian motion W. The term ‘Rough volatility’ refers to the idea that sample paths of the log volatility are rougher than the sample paths of Brownian motion, that is (Gatheral, Jaisson, & Rosenbaum, 2014).

Classical approaches (Heston, SABR…) suggested that,

with

(Gatheral, Jaisson, & Rosenbaum, 2014), (Bennedsen, Lunde, & Pakkanen, 2017) proposed across large financial data sets that

This is consistent with , where is a fractional Brownian motion with Hurst parameter and is a continuous Gaussian Process. The simplest rough volatility model and more natural for some Gaussian Volterra process

with B a Brownian motion and K is a singular kernel such that (Bennedsen, Lunde, & Pakkanen, 2017)

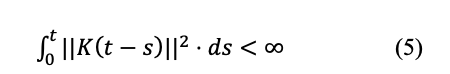
Horvath et al. (2019) suggested a Brownian Semi Stationary (BSS) process , with , where is strictly positive affine process independent of . This model could reproduce the VIX smile, which the other models could not reproduce for the VIX products.

Gatheral et al. (2014) for historical measures where the volatility is rough then;

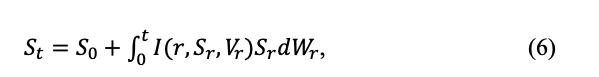
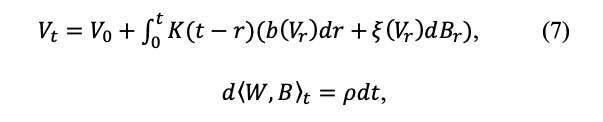
Here, the stochastic differential equation for X is a Volterra system generally, not Markovian.

According to Zhang & Zhuo (2014) β and σ depend on the past trajectory Xr for any t≥0 and r ∈ [0,t]. This would, for example, enable the inclusion of systems with delays.

Dupire (2009) and Gyongy (1986) calibrated the leverage function 1(·), which is of the form

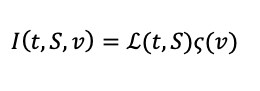
to ensure the model calibrated exactly to the European option prices.

This model depends only on the stock price and time, making this a perfect model for calibrating the European option prices, particularly path-dependent options.

Pricing function of the PPDE

The goal is to solve

via path-dependent PDEs and to propose a numerical scheme. Here is the infinite-dimensional stochastic process adapted to the filtration process

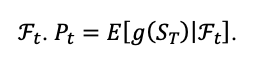
(Antoine & Mugad, 2019) assumes existence of a function

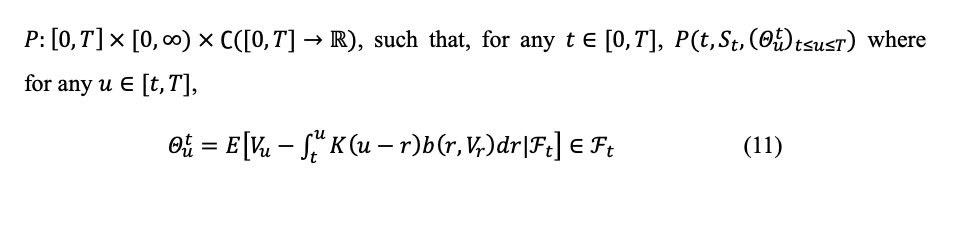
The option price has a unique solution to the linear path-dependent PDE

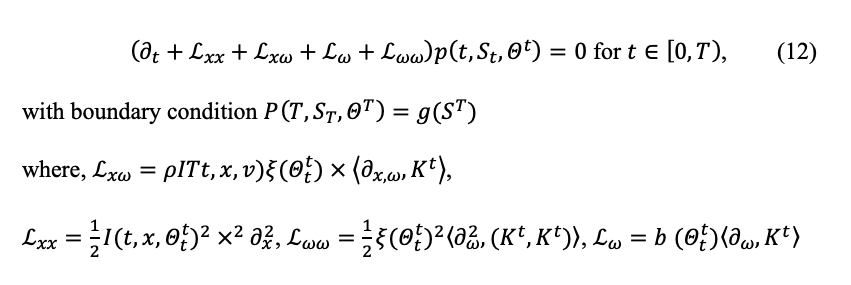
According to Ekren et al. (2016), uniqueness and its existence is guaranteed.

Where the space derivatives are defined as Gateaux derivatives given by

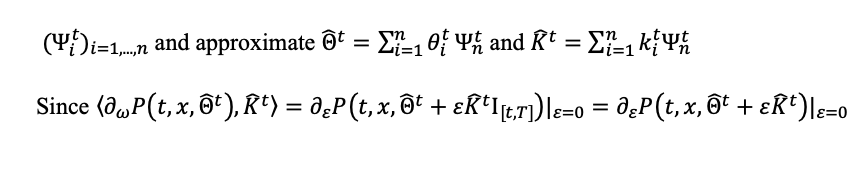
Discretization of the PPDE

From the option price unique solution of a PPDE equation (??) for each t ∈ [0,T], consider a basis of cadlag functions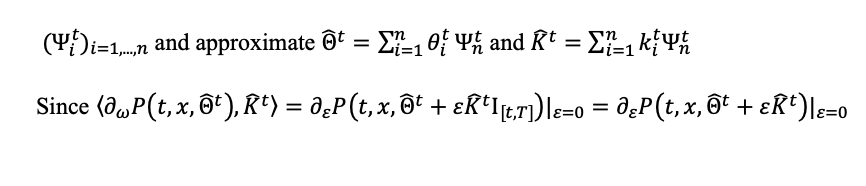

Then introducing the approximation

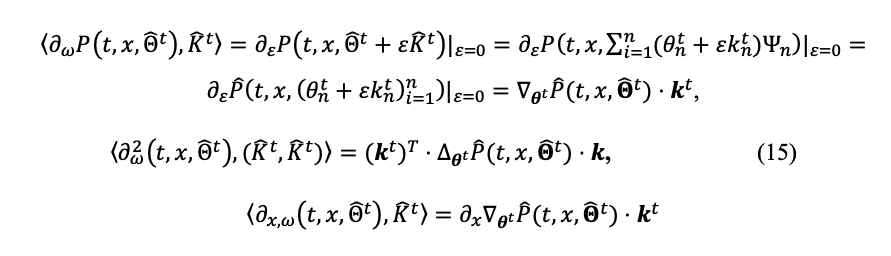
The PPDE becomes a very high-dimensional PDE

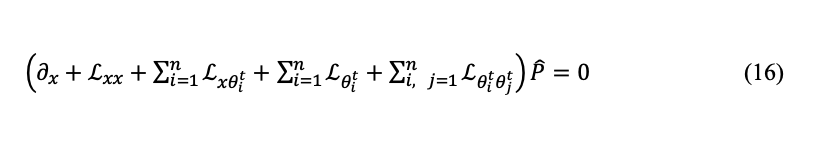
Where the differential operators are defined, for each i, j = 1,…, n as

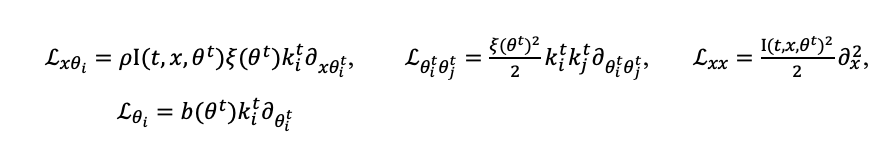
We can rewrite this system in a more concise way as

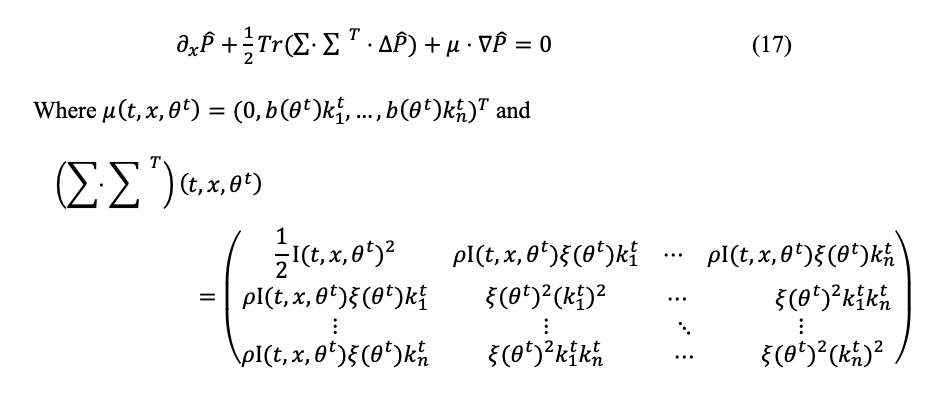
This is a very high-dimensional PDE.

The Backward stochastic differential equation (BSDE) formulation

One can associate a BSDE solution (X, Y, Z) to a given PDE where Y = P where this is an element of the BSDE written in backward form for any t ∈ [0,t]

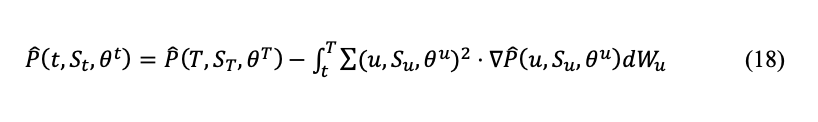
Discretizing (Euler) the backward SDE gives

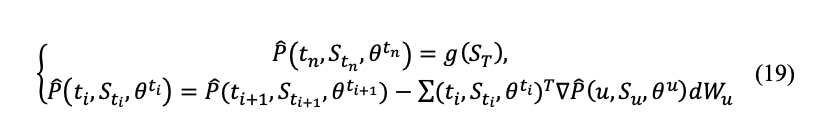
Simulation of the Volterra process was performed using a hybrid scheme as discussed by (Bennedsen, Lunde, & Pakkanen, 2017)

Han et al. (2018) computation via neural networks was used where at each time step, price and model parameters are known, but is unknown. This value is inferred by neural networks where is the number of layers per sub-network and is the number of neurons per layer.

The loss function to minimize is

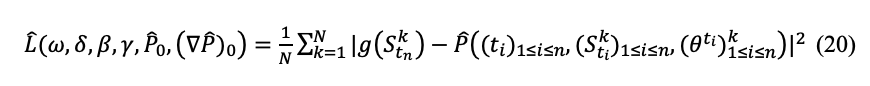
Conclusion

In conclusion, (Antoine & Mugad, 2019) presents a novel approach for modelling local stochastic volatility using deep probabilistic programming. The authors demonstrate the advantages of their approach over existing models, including its ability to capture complex nonlinearities and improve the accuracy of option pricing and risk management. While the paper may have limitations, such as its technical complexity and the need for further comparison with other models, it represents an essential contribution to quantitative finance. It may pave the way for future research in this area.

Overall, the paper presents an exciting and innovative approach to solving PDEs in finance using deep learning. The authors demonstrate the effectiveness of their approach in numerical experiments for option pricing under various rough stochastic volatility models.

However, there are a few limitations and potential areas for improvement in the paper. First, the authors use a relatively small number of training examples (5000) and do not perform a detailed sensitivity analysis on the hyperparameters of the neural network. This raises concerns about their results’ robustness and their approach’s generalizability to other models or settings.

Second, the paper lacks a comprehensive comparison of the proposed approach with existing methods for solving PDEs in finance, such as finite difference or finite element methods. While the authors briefly compare their results with the analytical solutions for some simple models, comparing their approach with other numerical methods in more realistic and complex settings would be more informative.

Finally, the paper does not discuss the potential limitations or drawbacks of using deep learning for solving PDEs. For example, deep learning approaches may suffer from overfitting or instability, especially in high-dimensional or ill-posed problems. Therefore, it would be helpful if the authors provided some insights or guidelines on how to mitigate these issues in practice.

References

Abi, J. E. (2019). Lifting the Heston Model. Quantitative Finance.

Antoine, J., & Mugad, O. (2019, June 6). Deep PPDEs for Rough Local Stochastic Volatility. Mathematics Subject Classification.

Bennedsen, M., Lunde, A., & Pakkanen, M. S. (2017). Decoupling the short-and-long-term behaviour of stochastic volatility. Energy Economics.

Dupire, B. (2009). Functional Ito Calculus.

Ekren, I., Touzi, N., & Zhang, J. (2016). Viscosity solution of fully nonlinear parabolic path-dependent PDEs: Part I. Annals of Probability.

Ekren, I., Touzi, N., & Zhang, J. (2016). Viscosity solutions of fully nonlinear parabolic path-dependent PDEs: Part II. Annals of Probability.

Gatheral, J., Jaisson, T., & Rosenbaum, M. (2014). Volatility is rough. Quantitative Finance.

Gyongy, I. (1986). Mimicking the one-dimensional marginal distributions of processes having an Ito differential. Probability Theory and Related Fields.

Hagan, P. S., Kumar, D., Lesniewski, A. S., & Woodward, D. E. (2002). Managing smile risk. The Best of Wilmott 1, 249-296.

Han, J., Jentzen, A., & E, W. (2018). Solving high-dimensional partial differential equations using deep learning. Proceedings of the Natural Academy of science.

Horvath, B., Jacquier, A., & Tankov, P. (2019). Volatility options in rough volatility models.

Omar, E. E., & Mathieu, R. (2019). The characteristic function of rough Heston Models. Math. Finance 29(1), 3-38.

Omar, E. E., Gatheral, J., & Mathieu, R. (2019). Roughening Heston. Risk, 84-89.

Omar, E. E., Masaaki, F., & Mathieu, R. (2016). The microstructural foundations of leverage effect and rough volatility. arXiv preprint arXiv: 1609.05177.

Ren, Z., & Tan, X. (2017). On the convergence of monotone schemes for path-dependent PDEs. Stochastic Processes and their Application.

Viens, F., & Zhang, J. (2019). A martingale approach for fractional Brownian motions and related path-dependent PDEs. Annals of Applied Probability.

Zhang, J., & Zhuo, J. (2014). Monotone schemes for fully nonlinear parabolic path-dependent PDEs. Journal of Financial Engineering.