Newton’s Laws of Motion

Introduction

Newton’s laws of motion are a fundamental part of physics. We will discuss in detail two of the three laws for this paper. We choose to look at the first and the third law closely.

First Law

Newton’s first law of motion states that if a body is at rest or is moving at a constant speed in a straight line, it will continue doing so unless acted upon by force. The first law is also popularly known as the inertia law. (Rosso & Svesko .2020 pp. 1-29). In basic terms, a body is supposed to remain in its current state beyond infinity if all the factors making it be at its current state remain constant. A ball resting on a football pitch should stay there unless an external factor changes that form. In the same way, a ball hit and traveling with the speed being constant and in a straight line should keep on traveling without stopping beyond infinite time unless an external force like friction acts upon it, resulting in a change.

Third Law

Newton’s third law of motion is also popularly known as the action and reaction law. The law states that the actions of two bodies on each other are always equal in magnitude and opposite in direction. The law emphasizes that there is always a similar and equivalent reaction for every step involving force. It takes place in the opposite direction of the party causing the action.

Pictorial Representation of the Laws

First Law

Picture 1 of 1^st law

This Picture is a good representation and can elaborate the first law. The Picture shows that when the forces balance, the objects remain at rest. The velocity is constant at 0 ms^-1. The acceleration is also 0ms^-2. When the objects are not subjected to change in direction or speed, they stay at rest forever. If these objects are subject to some force and start moving, their velocity changes from 0ms^-1. If the rate remains constant and in a straight line, implying that the acceleration is still 0ms^-2, the object will stay in motion forever. This will happen until another external force acts on the object in motion to cause an imbalance in the forces.

Picture 2 of 1^st law

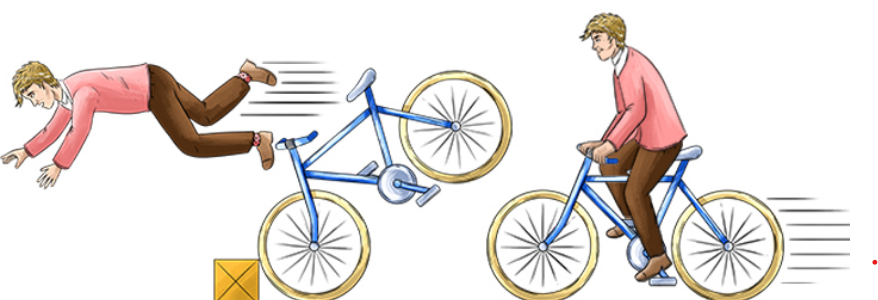
The above Picture can also elaborate on the first law of motion. The bicycle is moving at some constant velocity. The implication is that the acceleration is zero. If no external force affects the bicycle’s motion, it should keep on moving forever (Supeno et al .2018 .np). As illustrated, a stumbling block meets the rider on their way, causing an alteration in the velocity of the bicycle. The rider topples off to continue moving since the bike is the one that has been stopped. In essence, the rider should continue moving even with the stopping of the bicycle unless they also have external forces acting against their movement.

Newton’s Third law pictorial representation

1^st Picture

The law of action and reaction is well in practice in the above Picture. The Picture shows two gentlemen at opposite ends of a rope pulling each other. The two must remain faithful to the course for the status quo to be maintained, and the two individuals continue pulling one another. The fellow on the right side is pulling to his end, and the one on the left is pulling to his end, causing a reaction in the opposite direction (Wilson .2020 .np). The magnitude of the force is equal on both ends.

2^nd Picture

The Picture on our left shows a gentleman using a skating board. When he pushes his foot against the ground, he moves on his skateboard in the opposite direction (Shakir et al .2018 .np). The action is pushing the feet on the floor with the ground pushing back. This reaction makes him move forward in the opposite direction which he had pushed the ground. The magnitude of the reaction is equal to that of the action. A more intense push of the ground will result in a more significant reaction in that the skateboard will move at a faster speed in the opposite direction.

Math-based Problems to the above Laws and their Solutions

1^ST Law

Problem 1

A block of mass m slides on a table without friction. It is barred from moving in a rind of radius l, which is fixed to the table. At t= 0, the block is touching the ring and has a velocity of v₀ in the tangential direction. Find the velocity of the mass at subsequent times.

The constraint equation is r = l , i.e r’ = r” = 0

Equations of motion

M(r” –rθ²) = –mlθ² = -N

m (rθ” –2r’θ’) = mrθ” = –f

On eliminating N, we get

Θ” = -µθ’²

V(t) = lθ’

= v₀

1 + µv₀t/l

Problem 2

By solving Newton’s first law of motion, we find r(t)

r(t) = 0 Implying that the body is at rest always.

Generally,

Example

r(t) = (v_xt + x₀ ; 0; v_zt + z₀ –gt²/ 2) . The beside equation represents uniform motion in the x-direction with v_x as the velocity. The y-direction is in a state of rest and experiences uniform velocity v_z and a free fall in the gravitational field.

Mathematical Examples for the third law

Problem one

What is the total external force exerted on a 1120.00 Kg missile fired from a warship if the missile is accelerated at 1.99 x 10⁴ ms^-2? (b) What is the magnitude of the missile’s force exerted on the ship, and why is it so?

Solution

1. F_net­ = mass x acceleration

F_net­= 1120.00 kg x 2.40 x 10⁴ ms^-2

F_net­₌ 2.688 x 10⁷

2. The force exerted on the ship is also 2.688 x 10⁷N because, going by the third law, it is the opposite missile’s direction of motion.

Problem two

A Mathematics book is lying on top of a Geography book on a desk. The Mathematics and Geography books weigh 6 N and 20 N, respectively. Determine the action and action forces involved.

Solution

The weight of a Mathematics book is equivalent to the force exerted on the Mathematics book by the earth. We are going to represent this as;

F_EH  =-14j N.

The Mathematics book interacts only with the Geography book. Since the acceleration of the Mathematics book is zero, then the net force is also zero.

F_PH + F_EH=0, for F_PH being the force exerted by the Geography book on the Mathematics book. Thereby,

F_PH =-F_EH=0, whereby F_PH is the force exerted by the Geography book on the mathematics book, implying that,

F_PH =-F_EH= -(-14j)N = 14JN

The Geography book exerts an upward force of magnitude 14N on the Mathematics book. The Mathematics book has three forces exerted on it F_EP due to earth, F_HP  due to Mathematics book, and F_DP  due to desktop. For the Geography book weighs 20 N, F_EP  = -20j N. From Newton’s third law, F_HP = –F_PH  So, F_HP = -14j N and applying Newton’s second law to the Geography book we have that,

The summation of all forces is equivalent to zero.

i.e F_DP  + F_EP  + F_HP  = 0 So,

F_DP  = -(-20j) – (-14j) = 34j N

In conclusion, the desk exerts an upward force of 34 N on the Geography book, and we get to this by applying the third law of motion once and the second one twice.

Conclusion

In conclusion, the above discussion shows how vital Newton’s laws of motion are essential in our day-to-day lives. Examples exist on how the laws have been applied in basic practices like creating safety belts. Therefore, we must study more and strive to have a deeper understanding of the laws of motion.

References

Supeno, S., Subiki, S., & Rohma, L. W. (2018). Students’ Ability in Solving Physics Problems on Newtons’ Law of Motion.

Rosso, F., & Svesko, A. (2020). Novel aspects of the extended first law of entanglement. Journal of High Energy Physics, 2020(8), 1-29.

Shakir, S., Naran, S., Lowe, K. M., & Bartlett, S. P. (2018). Balancing distraction forces in the mandible: Newton’s third law of distraction. Plastic and Reconstructive Surgery Global Open, 6(9).

Wilson, J. (2020). Newtonian forces. The British Journal for the Philosophy of Science.