Analysis and Discussion
In mathematics lessons, factorization, quadratic expansion, and expanding squares help students to solve equations that frequently arise in almost all areas of mathematics. Generally, factorization plays a vital role in real life, which includes dividing something into equal parts, understanding time, comparing prices, making calculations during travel, and exchanging money. Solving quadratic equations is also crucial to students in the academic field and real-life issues. For example, it acquaints one with knowledge for calculating values for both moving and stationary objects. They can also be used to determine the loss or profit of a product in a particular business. Quadratic equations are primarily used in calculating speeds, profits, and areas. For example, construction engineers and workers apply quadratic equations to determine the area before starting any project. Thus, students must know quadratic equations to perform well in some careers.
The expansion of squares helps the students to practice critical thinking in solving other mathematical problems. Also, like any other mathematic lesson, expanding squares is very beneficial in solving real-life issues. Specifically, the expansion of squares is essential in finance, where one can use the knowledge to calculate the rates of returns in a business. Also, in some companies, the knowledge can be used to determine simple harmonic motions like springs and pendulums. Also, the expansion of squares helps to gain knowledge about other lessons like standard deviation which is used in probability theory and statistics. Hence, students need to learn the expansion of squares since it provides a foundation of knowledge on how other mathematical lessons can be solved. Hence, these mathematics lessons are intended to prepare students for other lessons like standard deviation since they provide foundation knowledge in solving them and help students perform complex analyses of real-life scenarios.
Even if factorization, quadratic expansion, and expanding squares provide one with basic knowledge in solving other complex math problems, pupils must also have the basic knowledge to perform well in the three lessons. There are three types of knowledge for these lessons: procedural knowledge, conceptual knowledge, and factual knowledge (Wilson, 2016). Bloom’s taxonomy showed various levels of knowledge that students should have to solve the three lessons. The taxonomy included knowledge, comprehension, application, analysis, synthesis, and evaluation.
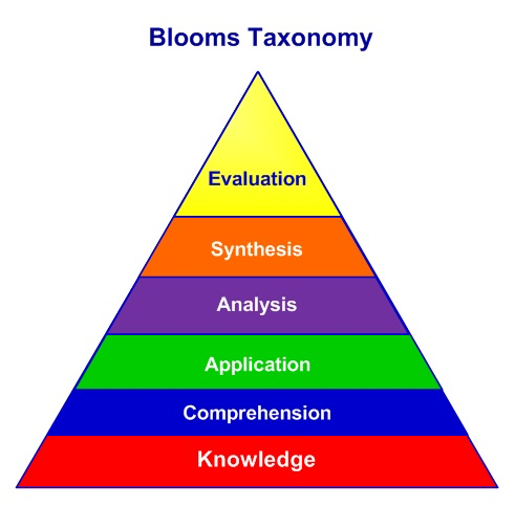
The taxonomy starts with knowledge which includes retrieving or remembering learned materials. For example, one must recall basic mathematical signs and their order in calculations to calculate factorization. The basic knowledge essential to students includes addition, subtraction, multiplication, and division. To enable one to recall previously learned knowledge, students need to have a good memory that can recall facts. The second stage is comprehension which involves the ability to grasp meaning from materials (Saputri, 2021). For any student to perform well in mathematics, this is the foundation of all calculations that even lead to the most complex problems in the subject.
After recalling materials that have been learned previously, it is essential to know how to apply them to the current problem. Hence, the other step, as contained in Bloom’s taxonomy, is the application, where one can use or implement the learned materials in new or real situations. This helps students to apply different methods and facts in real-life situations effectively. The analysis is the fourth step, which enables students to break down the concepts into components that are well understood to them. It helps them to understand the concepts well, enabling them to remember further solutions. Synthesis follows analysis and is beneficial since it combines the components to form a new coherent whole. Bloom’s taxonomy concludes with an evaluation which is also referred to as the ability to check the value of the material to conclude the measure and requires one to judge the result of the solution critically. This taxonomy, therefore, guides learners to calculate various mathematical problems and complexities.
Wilson (2016) identified three types of knowledge that help students to learn and solve various problems. First, factual knowledge is the most basic knowledge in a specific discipline (Rao, 2020, p. 10). For example, students must be familiar with essential terminologies and elements to solve a problem or understand a discipline. This knowledge is essential in remembering a rule by which one can decide if a problem satisfies a particular state. The factual knowledge primarily stems from students’ experiences in the class. Thus, this type of knowledge improves as one learns new things and may differ from one person to another depending on their memory level. If one remembers the rules that must be followed to solve a particular problem, it becomes easier for one to solve it. However, in factual knowledge, students know how specific rules work but not why they work. If a student is unfamiliar with essential facts about a topic, it implies they will not be able to solve the problem. Therefore, this knowledge is essential in solving any problem in a mathematics lesson. Also, factual knowledge helps in assessment as it shows the importance and relationship of one lesson with another and the need to learn them in a specific time.
The other type of knowledge is conceptual knowledge, also referred to as the knowledge of theories, structures, principles, generalizations, and classifications relevant to a specific disciplinary area. Conceptual knowledge enables the students to use what they know and helps them to grasp new ideas or topics (Davydov, 2020, p.228). It helps one to understand the inter-relationship between each lesson and enable them to build exemplar to understand the new topic. Generally, this knowledge plays a significant role in providing deep and connected learning experiences, which help understand the relationship between the lessons and how the learned lessons can be used to solve more complex problems. It is helpful to combine various materials to solve a problem more effectively.
List of References
Davydov, V. V. “The Psychological Characteristics of the Formation of Elementary Mathematical Operations in Children.” Addition and Subtraction, 2020, pp. 224-238.
Rao, N. J. “Outcome-based Education: An Outline.” Higher Education for the Future, vol. 7, no. 1, 2020, pp. 5-21.
Saputri, N.L., 2021. Analysis of Reading Comprehension Questions Based on Higher Order Thinking Skills in Cognitive Domain Of Revised Bloom’s Taxonomy. Jurnal Ilmiah Wahana Pendidikan, 7(2), pp.27-37.
Wilson, L.O., 2016. Anderson and Krathwohl–Bloom’s taxonomy revised. Understanding the New Version of Bloom’s Taxonomy.
 write
write