Abstract:
This report compares regression models applied to two distinct datasets: Boston Housing and Sales of Advertising. The purpose is to gauge the efficacy of different regression techniques in forecasting housing prices and sales dependent on advertising budget. Some models considered for evaluation are Linear Regression, Decision Tree Regression ( fully grown and pruned), and K-Nearest Neighbors( KNN). We also perform the analysis and model evaluation to determine the advantages and disadvantages of different regression techniques in light of these diverse datasets. Through the analysis of the performance characteristics of each model, the fully grown tree emerged to be the best model for performing the prediction with lower RMSE and MAE.
Introduction
Regression analysis constitutes a base statistical method applied in different industries to predict a continuous response variable from one or more explanatory variables. It applies at every level of all the state’s economies, financial institutions, social sciences sectors, and even to entities beyond the reach of humankind. It provides explanations and understanding of the variables; thus, the users can make the best decisions if they implement the variables. To this end, the report undertakes a comparative appraisal of regression models utilized in connection with two separate datasets – the aim is to assess the models as price-forecasting and sales-prediction tools.
Under investigation are two datasets that emanate from different domains, each posing unique challenges and prospects for predictive modeling. The first dataset is about housing economics and has been obtained from the U.S. Census Service; its features include housing characteristics in Boston, Massachusetts. This dataset’s dependent variable of focus is median home values (MEDV), a critical factor in real estate assessment and market review.
The second dataset is centered on marketing and advertising, covering the sales figures of a particular product among the various media such as TV, radio, and newspaper. Analyzing the effect of advertising expenses on sales performance is fundamental for companies aiming to improve their marketing strategies and spend their efforts appropriately.
Data Description
Boston Housing Dataset:
In this dataset, the U.S Census Bureau provides information about Boston housing in Massachusetts. The set consists of 13 features like crime rate, proportion of non-retail business acres per town, average number of rooms per dwelling, and median value of owner-occupied homes (MEDV) (Hoxha, 2024). The indicator of the target is the median value of owner-occupied houses (MEDV).
Linear Regression Model: Linear regression model was built using both stats models.api and the learn package. stats models.API results include Beta coefficients and p-values for each predictor were established. P-values assist in determining the significance of every predictor. P-values reveal that some predictors are significant (p < 0.05), and others are not. As an illustration, RM, PTRATI, O, and LSAT have low p-values, which signify they are significant predictors. The actual value, the predicted value, and the residual values for the housing prices are shown below:

Advertising Sales Dataset:
The dataset represents the sales figures of a particular product based on advertising spending on three different media: TV, radio, and newspaper. This dataset contains three features: The advertising expenditure of TV, radio, newspapers, and sales. The target variable is the sales. The linear regression model was built using the sklearn package. The model was trained and evaluated using RMSE and MAE. The actual values, predicted values, and residual values are shown below.

Methodology
Boston Housing Dataset:
We implemented Linear Regression using both stats models. API and clear, and Decision Tree Regression with two variations: trees looked full-grown and pruned.
The evaluation metrics of models include Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE)
Advertising Sales Dataset:
The dataset represents the sales figures of a particular product based on advertising spending on three different media: TV, radio, and newspaper sales. The dataset is composed of 3 features: Advertising expenditure on TV, advertising expenditure on radio, advertising expenditure on newspaper, and sales. The dependent variable is the sales amount.
Also, we used K-Nearest Neighbors (KNN) Regression with feature scaling using StandardScaler (Kohli et al., 2020). Model evaluation metrics involve RMSE and MAE.
Results and Discussion
4.1 Boston Housing Dataset:
Linear Regression – RMSE: 4.772599769922687 MAE: 3.1113773882381848
Fully Grown Tree – RMSE: 2.996632096465735 MAE: 2.217647058823529
Pruned Tree – RMSE: 3.673046832398878 MAE: 3.0071469760281424
The best model is: Fully Grown Tree
Fig 4: Shows the regression summary analysis results for Boston Housing
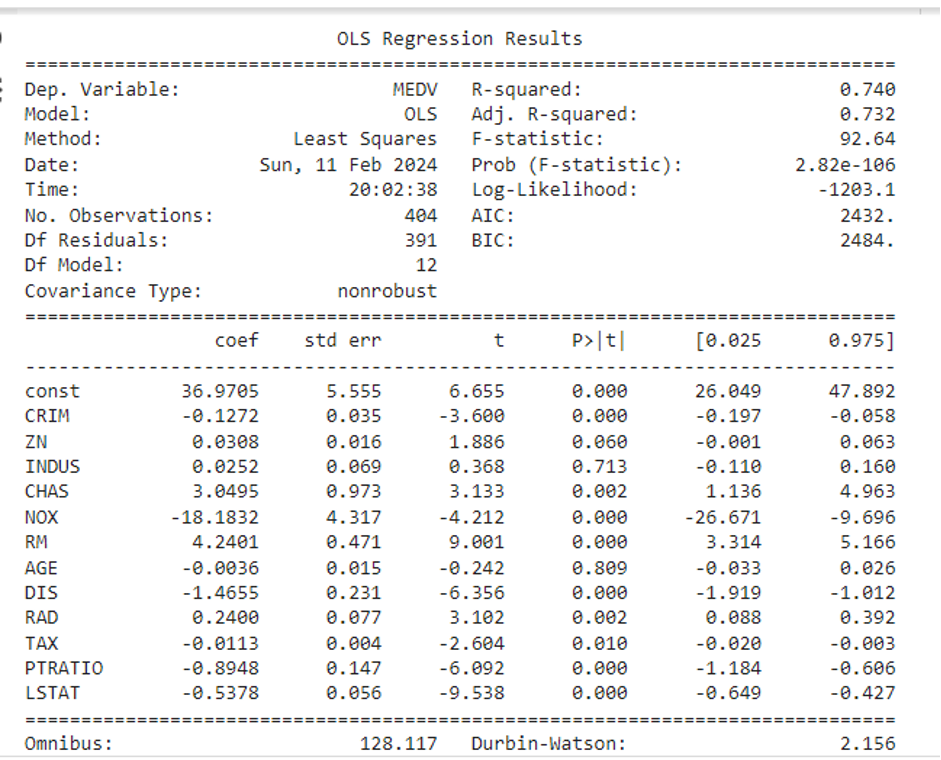
4.2 Advertising Sales Dataset:
Linear Regression – RMSE: 1.7052146229349223 MAE: 1.2748262109549338
Fully Grown Tree – RMSE: 1.8444511378727275 MAE: 1.24
Pruned Tree – RMSE: 2.279765895641708 MAE: 1.7668252387726064
KNN model – RMSE 1.726276339408033 MAE 1.4074999999999993
The best model is Linear Regression
While the Fully Grown Tree model for the Boston Housing dataset and Linear regression analysis prove to be the best performer in this analysis, it is essential to consider other factors such as model complexity, interpretability, and computational efficiency for real-world deployment. Future research could explore ensemble methods or advanced regression techniques to further enhance predictive accuracy (Yuan et al., 2024). Continuous monitoring and validation of the chosen model’s performance are recommended to ensure its effectiveness.
Conclusion
As per the evaluation metrics, the Fully Grown Tree is the best model for the Boston Housing dataset; however, Linear Regression performs the best for the Advertising Sales dataset. This indicates that a regression model may differ across datasets and predictive tasks. This report gives a detailed comparison of regression models employed in predicting housing prices and advertising sales, analyzing the strengths and weaknesses of each method.
Recommendations
Research on feature engineering and selection methods needs to be done further to help improve the models’ predictive performance. Ensemble methods, e.g., Random Forest or Gradient Boosting, may improve the prediction accuracy. Regular monitoring and updating of the predictive models are advisable to maintain relevance and effectiveness.
References:
Hoxha, V. (2024). Comparative analysis of machine learning models in predicting housing prices: a case study of Prishtina’s real estate market. International Journal of Housing Markets and Analysis.
Kohli, S., Godwin, G. T., & Urolagin, S. (2020). Sales prediction using linear and KNN regression. In Advances in Machine Learning and Computational Intelligence: Proceedings of ICMLCI 2019 (pp. 321–329). Singapore: Springer Singapore.
Yuan, S., Kroon, B., & Kramer, A. (2024). Building prediction models with grouped data: A case study on the prediction of turnover intention. Human Resource Management Journal, 34(1), 20-38.
Appendix:
The link below provides the code used for the data preprocessing, model implementation, and evaluations of both datasets. https://colab.research.google.com/drive/1O0wO52jUsDVdk9KOV_46TG6yjOZs_XqY?usp=sharing
 write
write