INTRODUCTION
This study seeks to investigate the creditworthiness of customers in Taiwan, as one of the primary goals of a lending institution is to keenly assess and manage both the customer and the credit by ensuring that the credit is available, evaluating the related risks, optimizing the returns, and most importantly addressing customer’s payment defaults. The majority of lending institutions have aimed to ensure that they have full control of the risks associated with providing loans; here, associating independent third-party evaluations to assess the creditworthiness of clients has helped mitigate the risks related to credit defaults. Evaluating the creditworthiness of an individual is of utmost importance for banks and financial organizations. The complexity of assessing credit risk depends on a number of variables, such as an individual’s financial situation, the state of the economy, and anticipated market volatility. Traditional approaches to assessing credit risk have been employed for an extended period. Still, they may not be well equipped to handle the vast and intricate data that is accessible in the present digital age. This project aims to create and validate a credit risk assessment mechanism using the Support Vector Machine. This learning technique improves banks’ ability to detect credit-related difficulties by effectively utilizing the ample data accessible to individuals. The suggested methodology seeks to leverage machine learning techniques to provide a comprehensive assessment of individuals’ creditworthiness. The objective of this method is to reduce the probability of loan defaults by empowering banks to make informed and tactical lending choices.
Furthermore, the possible implementation of such a credit risk assessment system could provide multiple benefits to financial institutions. The installation of this system is expected to result in enhanced credit risk evaluation, thereby reducing the bank’s non-performing loan ratio and increasing overall profit margins. The analysis will be conducted in SAS enterprise miner, where the results will be presented in both table format and graphs. The dataset for this research was retrieved via the link Default of Credit Card Clients Dataset (kaggle.com). It consisted of 25 features with 30000 observations, of which there was a single binary target, nine nominal inputs, and 14 interval inputs. The descriptive statistics for the continuous variables were as follows.
Table 1 Descriptive Statistics Summary
| Variable | Mean | Deviation | Missing | Missing | Minimum | Median | Maximum | Skewness | Kurtosis |
| AGE | 35.4855 | 9.217904 | 30000 | 0 | 21 | 34 | 79 | 0.732246 | 0.044303 |
| BILL_AMT1 | 51223.33 | 73635.86 | 30000 | 0 | -165580 | 22381 | 964511 | 2.663861 | 9.806289 |
| BILL_AMT2 | 49179.08 | 71173.77 | 30000 | 0 | -69777 | 21197 | 983931 | 2.705221 | 10.30295 |
| BILL_AMT3 | 47013.15 | 69349.39 | 30000 | 0 | -157264 | 20088 | 1664089 | 3.08783 | 19.78326 |
| BILL_AMT4 | 43262.95 | 64332.86 | 30000 | 0 | -170000 | 19052 | 891586 | 2.821965 | 11.30932 |
| BILL_AMT5 | 40311.4 | 60797.16 | 30000 | 0 | -81334 | 18104 | 927171 | 2.87638 | 12.30588 |
| BILL_AMT6 | 38871.76 | 59554.11 | 30000 | 0 | -339603 | 17068 | 961664 | 2.846645 | 12.27071 |
| LIMIT_BAL | 167484.3 | 129747.7 | 30000 | 0 | 10000 | 140000 | 1000000 | 0.992867 | 0.536263 |
| PAY_AMT1 | 5663.581 | 16563.28 | 30000 | 0 | 0 | 2100 | 873552 | 14.66836 | 415.2547 |
| PAY_AMT2 | 5921.164 | 23040.87 | 30000 | 0 | 0 | 2009 | 1684259 | 30.45382 | 1641.632 |
| PAY_AMT3 | 5225.682 | 17606.96 | 30000 | 0 | 0 | 1800 | 896040 | 17.21664 | 564.3112 |
| PAY_AMT4 | 4826.077 | 15666.16 | 30000 | 0 | 0 | 1500 | 621000 | 12.90498 | 277.3338 |
| PAY_AMT5 | 4799.388 | 15278.31 | 30000 | 0 | 0 | 1500 | 426529 | 11.12742 | 180.0639 |
| PAY_AMT6 | 5215.503 | 17777.47 | 30000 | 0 | 0 | 1500 | 528666 | 10.64073 | 167.1614 |
The default to payment next month was our binary target variable. From the dataset, we can see that 77.88% of the customers are not expected to default payment, whereas 22.12% of the customers were expected to default payment. This shows a high imbalance on the target variable, which, once we determine the best SVM model, will assign a 22.12% cutoff, denoting the true positives.
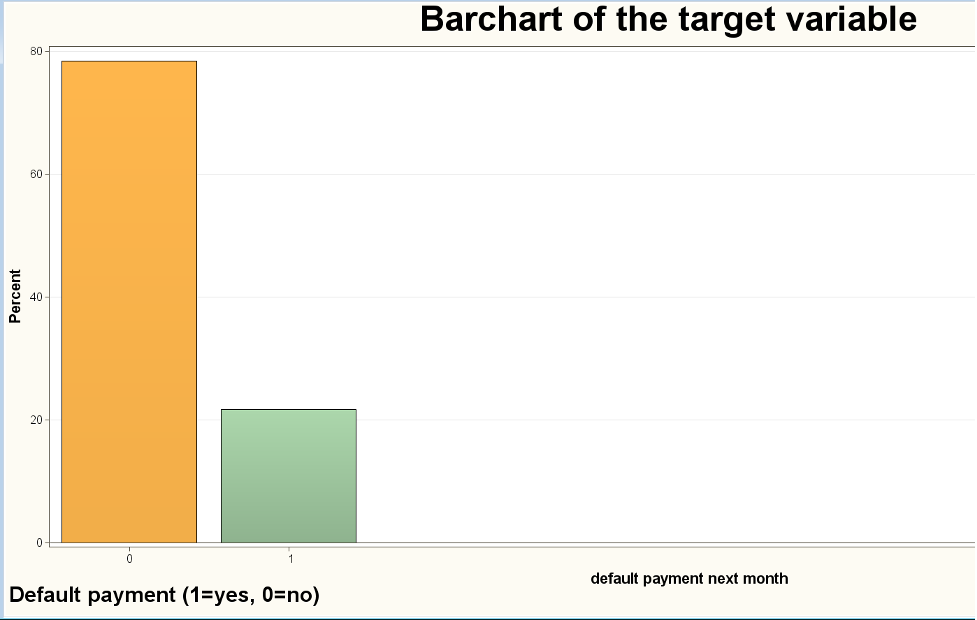
Figure 1 Bar chart of the target variable
A chi-square test was conducted to determine whether there was an association between the target variable and the input nominal variable. Where based on the results p-value, we see that the association is statistically significant as the p-values are lesser than the assumed alpha 0.05
Table 2 Chi-square summary
| Input | Chi-Square | Degrees of freedom | Prob |
| PAY_0 | 5365.9650 | 10 | <.0001 |
| PAY_2 | 3474.4668 | 10 | <.0001 |
| PAY_3 | 2622.4621 | 10 | <.0001 |
| PAY_4 | 2341.4699 | 10 | <.0001 |
| PAY_5 | 2197.6949 | 9 | <.0001 |
| PAY_6 | 1886.8353 | 9 | <.0001 |
| EDUCATION | 163.2166 | 6 | <.0001 |
| SEX | 47.9054 | 1 | <.0001 |
| MARRIAGE | 35.6624 | 3 | <.0001 |
Data Cleaning and Preparation
Support vector machine(SVM) was implemented on the binary target variable default payment for the next month where 0 implied the customer didn’t make any default, whereas 1 is the case where the client actually made a default in payment for the next month. Here, we see that the SVM performance was better with a large number of features and a small sample size, hence the need for data partitioning. The first preparation conducted was to split the data into a stratified training, validation, and testing set. Putting in mind that the target variable was imbalanced, we used a split ratio of 4:3:3 with 40% of the data being allocated to the training set, that is, 12000 observations and 30% of the data being given to both the validation set and testing set being 9000 observations each. Here, the goal was to minimize the data sample as much as we could. The next step was to transform the continuous features by standardizing them so as to assume normality (zero skew and zero kurtosis) and also to place them on a relative scale. Conversion of all the features to numeric variables was also implemented. We then proceeded to check for any missing data present, and we came to the conclusion that there was no missing data current, hence no need to input the data.
Predictive models Developed
This section will look at the results generated for the different SVM models, which varied based on kernels which were the linear kernel and the polynomial kernel both for interior point settings, and the polynomial kernel, the sigmoidal kernel, and the Radial basis kernel for active point setting. Here, we developed two scenarios to test the performances of each of the models. Scenario one was without data preparation, and the second scenario was with data preparation, whose results were as follows.
Table 3 Model summary without preparation
| Model Description | Validation Misclassification Rate | Train Average Squared Error | Train Misclassification Rate | Valid Average Squared Error |
| HP SVM Polynomial Interior | 0.18133 | 0.16269 | 0.17926 | 0.16484 |
| HP SVM Polynomial 4 active | 0.18156 | 0.20465 | 0.17326 | 0.20708 |
| HP SVM Radial Active | 0.18700 | 0.14835 | 0.18852 | 0.14858 |
| HP SVM Linear Interior | 0.19056 | 0.15511 | 0.19285 | 0.15487 |
| HP SVM Sigmoid 1 | 0.29467 | 0.20380 | 0.29044 | 0.20691 |
| HP SVM Sigmoid 2 | 0.30056 | 0.21052 | 0.30144 | 0.21322 |
Here, we will look to monitor the model’s performance based on the misclassification rate where the model chosen in this case is the hyper-tuned SVM polynomial interior with a polynomial degree of three, which had a validation misclassification rate of 0.18133. We see that only 18.13% of the validation observations were incorrectly predicted, but this needs to be more accurate as the target variable is heavily imbalanced, hence the introduction of the cutoff node to the best model.
Table 4 Model summary with preparation
| Model Description | Validation Misclassification Rate | Train Average Squared Error | Train Misclassification Rate | Valid Average Squared Error |
| HP SVM interior point-polynomial | 0.18311 | 0.18250 | 0.17135 | 0.18727 |
| HP SVM Active set Radial | 0.19167 | 0.14421 | 0.18660 | 0.14740 |
| HP SVM active polynomial p=4 | 0.19344 | 0.19605 | 0.14310 | 0.20595 |
| HP SVM interior point -linear | 0.20056 | 0.15400 | 0.19910 | 0.15448 |
| HP SVM Active Sigmoid 1 | 0.22056 | 0.18362 | 0.22152 | 0.18452 |
| HP SVM Sigmoid 2 | 0.22122 | 0.22106 | 0.22110 | 0.22118 |
Similar to the model summary above, we also check on the misclassification rate for the SVM model with data preparation implemented. Here, we see that the hyper-tuned SVM polynomial interior with a polynomial degree of three was also the model with the least misclassification rate of 0.18311.
Results
In this section will look at the accuracies for each model in each scenario with their respective confusion matrix for the best models. The results were as follows
| Model Description | Training accuracies without preparation | Training accuracies with preparation |
| HP SVM interior point-polynomial | 0.8207 | 0.8287 |
| HP SVM Active set Radial | 0.8115 | 0.8134 |
| HP SVM active polynomial p=4 | 0.8267 | 0.8569 |
| HP SVM interior point -linear | 0.8072 | 0.8009 |
| HP SVM Active Sigmoid 1 | 0.7096 | 0.7785 |
| HP SVM Sigmoid 2 | 0.6986 | 0.7789 |
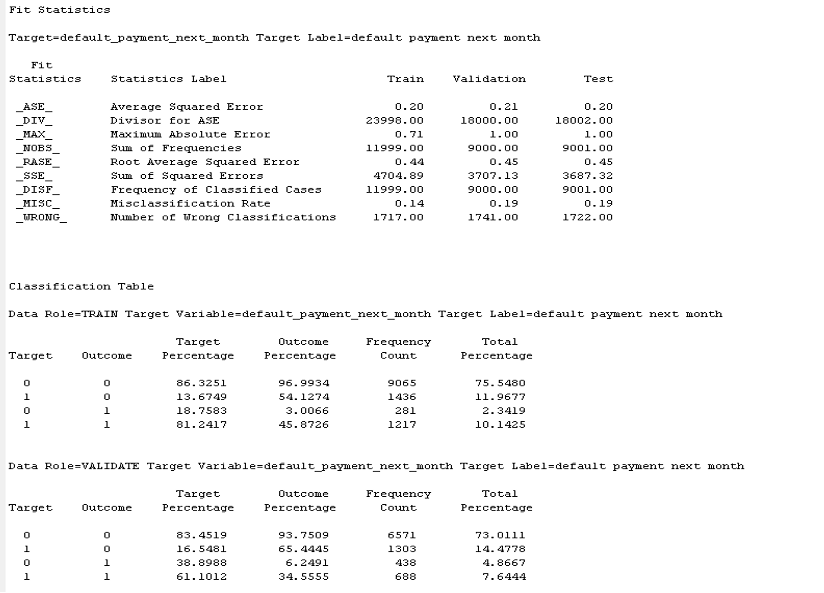
Here, we see, based on the model summary for each scenario, that the hyper-tuned SVM active polynomial with a polynomial degree of 4 had the highest accuracy of 0.8569, that’s 85.69% accurate predictions.
Conclusion
In conclusion, based on the model result, we see that the best SVM model was the HP SVM active polynomial p=4 as it had the highest accuracy score of 0.8569, which was the fraction of correct predictions and a misclassification score of 0.19344. We also see, based on the classification report, that 81.24% were classified as 1:1, with 83.45% being classified as 0:0. This shows a better balance in the target variable.
Reference
- Caplinska, A., & Tvaronavičienė, M. (2020). Creditworthiness is placed in credit theory and its methods of evaluation. Entrepreneurship and sustainability issues, 7(3), 2542.
- Shen, G., & Du, Y. (2022, March). Research on the Construction of a Personal Credit Risk Assessment Index System based on PCA. In CIBDA 2022; 3rd International Conference on Computer Information and Big Data Applications(pp. 1-4). VDE.
- Tao, W. (2010, May). Evaluation and Construction of Individual credit evaluation system based on a third-party e-commerce transaction platform. In 2010 International Conference on E-Business and E-Government(pp. 283-286). IEEE.
Appendix
Table 5 Data description
| Feature | Description |
| ID | The ID of each client |
| LIMIT_BAL | Amount of given credit in NT dollars (includes individual and family/supplementary credit |
| SEX | Gender (1=male, 2=female) |
| EDUCATION | (1=graduate school, 2=university, 3=high school, 4=others, 5=unknown, 6=unknown) |
| MARRIAGE | Marital status (1=married, 2=single, 3=others) |
| AGE | Age in years |
| PAY_0 | Repayment status in September, 2005 (-1=pay duly, 1=payment delay for one month, 2=payment delay for two months, … 8=payment delay for eight months, 9=payment delay for nine months and above) |
| PAY_2 | Repayment status in August 2005 (scale same as above) |
| PAY_3 | Repayment status in July 2005 (scale same as above) |
| PAY_4 | Repayment status in June 2005 (scale same as above) |
| PAY_5 | Repayment status in May 2005 (scale same as above) |
| PAY_6 | Repayment status in April 2005 (scale same as above) |
| BILL_AMT1 | Amount of bill statement in September 2005 (NT dollar) |
| BILL_AMT2 | Amount of bill statement in August 2005 (NT dollar) |
| BILL_AMT3 | Amount of bill statement in July 2005 (NT dollar) |
| BILL_AMT4 | Amount of bill statement in June 2005 (NT dollar) |
| BILL_AMT5 | Amount of bill statement in May 2005 (NT dollar) |
| BILL_AMT6 | Amount of bill statement in April 2005 (NT dollar) |
| PAY_AMT1 | Amount of previous payment in September 2005 (NT dollars) |
| PAY_AMT2 | Amount f previous payment in August 2005 (NT dollars) |
| PAY_AMT3 | Amount of previous payment in July 2005 (NT dollars) |
| PAY_AMT4 | Amount of previous payment in June 2005 (NT dollars) |
| PAY_AMT5 | Amount of previous payment in May 2005 (NT dollars) |
| PAY_AMT6 | Amount of previous payment in April 2005 (NT dollars) |
| default payment next month | Default payment (1=yes, 0=no) |
 write
write