Introduction
Entropy is qualitatively referred to as a measure of the extent of how atomic and molecular energy become more spread out in a process in terms of thermodynamic quantities. Similarly, it is the subject of the Second and Third laws of thermodynamics, which describe the variation in the Entropy of the Universe according to the system and settings. The Entropy of substances, correspondingly the behaviour of a system, is described in terms of thermodynamic properties like temperature, pressure, and heat capacity taking into account the state of equilibrium of the systems.
The second law of thermodynamics points out the irreversibility of natural processes whereby the Entropy of any isolated system never drops since, in a natural process of thermodynamics, the totality of the entropies of the interacting thermodynamic systems escalates. Thus, reversible processes are theoretically helpful and convenient but do not occur naturally. It is deduced from this second law that it is impossible to build a device that functions on a cycle with the sole effect of transferring heat from a cooler to a hotter body.
Based on the third law of thermodynamics, the Entropy of a system approaches a constant value as the temperature approaches absolute zero. Thus, it is impossible for any process, no matter how ideal, to decrease the temperature of a system to absolute zero in a restricted number of phases. At zero point for the thermal energy of a body, the motion of atoms and molecules reaches its minimum.
Entropy is integrated into the new approach to generate advanced metallic materials in chemical engineering, concentrating on the crystal structure’s high symmetry and strength. In thermodynamics and statistical physics, Entropy entails a quantitative measure of the disorder or energy to perform work in a system. The disorder is the actual number of all the molecules making up the thermodynamic system in a state of specified macroscopic variables of volume, energy, heat and pressure.
Mathematically: Entropy = (Boltzmann’s constant k) x logarithm of the number of possible states
S = kB logW
The equation relates the system’s microstates through W to its macroscopic state over the Entropy S. In a closed system, Entropy does not decline; as a result, Entropy increases irreversibly in the Universe. In an open system like that of a growing tree, the Entropy can decline, and the order can increase, however, only at the expense of an upsurge in Entropy somewhere else, like in the Sun (Connor, 2019).
An increase in Entropy in the cold body greatly offsets the decrease in the Entropy of the hot body. The SI unit of Entropy is J/K. According to Clausius, the Entropy was demarcated over the change in Entropy S of a system when an amount of heat Q is introduced by a reversible process at constant heat T in kelvins.
∆S = S2 – S1 = Q/T
The Q/T quotient is associated with increased disorder, whereby a higher temperature implies greater randomness of motion. However, engineers apply specific Entropy (s) in thermodynamic enquiry. The specific Entropy of a given material is its Entropy per unit mass obtained by the equation: s = S (J)/m (kg).
Entropy Change
Considering that Entropy measures energy dispersal, the change considers how much energy is spread out in a process at a specific temperature. “How much” refers to the energy input to a system. “How widely” entails the processes in which the preliminary energy in a system is unaltered, but it spreads out more like in the expansion of an ideal gas or mixture (Jensen, 2004). The change in Entropy applies to a wide range of chemical reactions whereby bonds are broken in reactants and formed in products with more molecules, undergo a phase change, or even mix with reactants.
When heat is introduced to the solution to the normal boiling point of a solvent, its molecules will not escape to the vapour phase in the equivalent amounts of the pure solvent at that temperature to match the atmospheric pressure. As a result, it is essential to raise the temperature of solutions above the solvent’s normal boiling point to cause boiling. Likewise, when a solution is cooled to the solvent’s normal freezing point, the molecular energy of the solvent is so dispersed that the molecules do not freely arrange to form a solid as in the pure solvent. Therefore, the temperature of the solution should be lowered below the normal freezing level to avoid the compensation of the lesser energy of the solvent molecules for their more excellent dispersion and slowly move to escape the solution to form a solid.
How to Calculate the Entropy Change for a Chemical Reaction
The energy emitted or absorbed by a reaction is monitored by taking note of the change in temperature of the surroundings and used in defining the enthalpy of a reaction with a calorimeter. Since there is no analogous easy manner to experimentally define the change in Entropy for a reaction, in a situation where it is known that energy is going into or exiting a system, variations in internal energy not accompanied by a temperature alteration reflect deviations in the Entropy of the system.
For instance, in the melting point of ice, where water is at °0C, and 1 atm pressure, water’s liquid and solid phases are in equilibrium.
H2O(s) →H2O (l)
In this equation, if a small amount of heat energy is introduced into the system, the equilibrium would move slightly to the right towards the liquid state. Similarly, removing a small amount of energy from the system would favour equilibrium towards more ice (left). Nonetheless, both processes do not involve temperature change unless all the ice is melted or the liquid water is frozen into ice; hence a state of equilibrium no longer exists. The temperature changes are accounted for in determining the entropy change in the system. The change in Entropy in a chemical reaction is determined by combining heat capacity measurements with measured values of synthesis or vaporization enthalpies, which encompasses integrating the heat capacity over the temperature range and adding the enthalpy variations for phase transitions. Similarly, subtracting the sum of the entropies of the reactants from that of products is a viable approach.
ΔS reaction=∑ΔS products−∑ΔS reactants
How Entropy Affects the Efficiency of Chemical Engineering Systems
Based on the second law of thermodynamics that the Entropy of an isolated system cannot decline with time, Entropy affects the efficiency of chemical engineering systems. As a result, any process that encompasses a reduction in Entropy, like converting heat energy to work, must go along with a rise in Entropy in a different place. The efficiency of the process is the ratio of helpful work yield to heat input which is never hundred per cent due to some heat loss ensuing from entropy increase.
Applications of Entropy in Chemical Engineering
In measuring the randomness of a system, Entropy plays a significant role in defining the direction and feasibility of chemical reactions in chemical engineering. In Gibb’s free energy equation, enthalpy and Entropy are combined to predict the spontaneity of a reaction. The second law of thermodynamics is applied in computing the efficiency of heat engines, refrigerators and heat pumps since the Entropy constantly increases in an isolated system (Elliot et al., 2012). Similarly, the Entropy of fusion, vaporization and Entropy of mixing is utilized to understand phase transitions and mixing of substances. Additionally, Entropy develops a conceptual comprehension of thermodynamics and its relationship with other scientific concepts of energy, temperature, pressure and volume.
Literature Review
The simple correlation of Entropy with the constraint of motion enables rationalization of the qualitative rules for predicting the net entropy change in simple chemical reactions. For instance, when adding a solid solute to a solvent, despite the change in size or volume of the substances, the emotional energy of each of the molecules becomes more dispersed in the ensuing solution (Lambert, 2002). Thus the Entropy of every component has increased because the solvent in any solution possesses its more dispersed emotional energy, and its molecules are less likely to exit that solution compared to solvent molecules in pure solvent.
The specific Entropy of a substance could be pressure, temperature, and volume; however, such properties cannot be quantified directly. Since Entropy measures the energy of a material that is no longer available to carry out practical work, it tells volumes about the worth of the extent of heat transferred in doing work. Generally, the levels of a substance and the interactions between its properties are most commonly displayed on property diagrams with specific dependencies amid properties. For instance, the Temperature-entropy diagram shown in Figure 1 is often used to analyze energy transfer system cycles in thermodynamics to visualize variations in temperature and specific Entropy in a process. As a result, the amount of work the system performs, and the amount of heat added or removed from the system can be visualized.
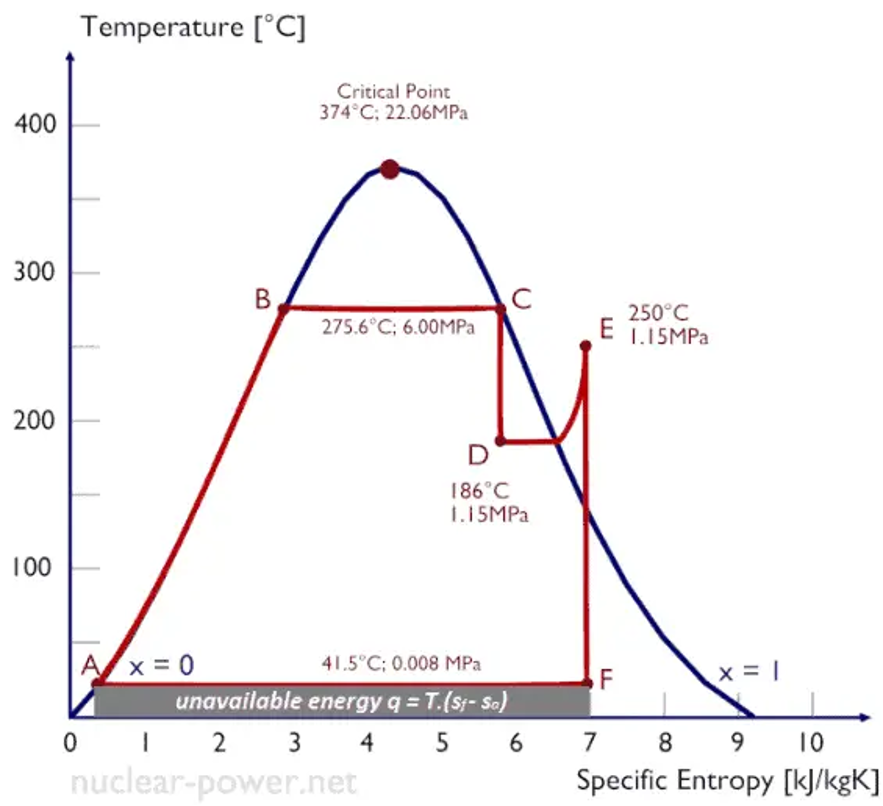
Figure 2: T-s diagram of Rankine Cycle
Source: (Connor, 2019)
The vertical line on the diagram depicts anisentropic process, while the horizontal line illustrates an isothermal process a. For instance, isentropic processes in an ideal state of compression in a pump entail compression in a compressor and expansions in a turbine useful in power engineering in thermodynamic cycles of power plants. Real thermodynamic cycles have in-built energy losses due to compressors and turbines’ inefficiency. It is evident from general experience that ice melts, iron rusts, and gases mix. Nonetheless, the quantity of Entropy helps determine whether a given reaction would take place, noting that the reaction rated is independent of spontaneity.
While a reaction could occur spontaneously, the rate could be so slow that it is not effectively observable when the reaction happens, like in the spontaneous conversion of diamond to graphite. Therefore, the apparent discrepancy in the change of Entropy between irreversible and reversible processes is clarified when considering the variations in Entropy of the surroundings and system, as designated in the second law of thermodynamics. In a reversible process, the system takes on a continuous succession of equilibrium states whereby its intensive variables of chemical potentials, pressure and temperature are continuous from the system to the surroundings, and there is no net change (Fairen et al., 1982). Real processes are generally irreversible; hence, reversible is a limiting case. From the analysis of thermal engines, reversible processes take an extremely long time and cannot generate power.
A new approach to thermodynamic Entropy entails a model for which energy extents throughout macroscopic material and is shared among microscopic storage modes, the nature of energy spreading and sharing fluctuations in a thermodynamic process and the rate of energy spreading and sharing is greatest at thermodynamic equilibrium. The degree of energy spreading and sharing is assigned function S which is identical to Clausius’ thermodynamic Entropy. In the second law of thermodynamics, a spontaneous process can only progress in a definite direction and equal amounts of energy are involved irrespective of the viability of the process. Experiments have shown that only a percentage can be transformed into work when heat energy is transferred to a system (Dincer & Cengel, 2001). The second law institutes the quality variance in diverse energy forms. It elucidates why some processes can happen spontaneously while others cannot hence a trend of variation and is often presented as an inequality.
All physical and chemical spontaneous processes ensure to maximize Entropy through increased randomized conversion of energy into a less accessible form. A direct concern of fundamental significance is the inference that at thermodynamic equilibrium, a system’s Entropy is at a relative maximum since a further increase in disorder is impossible without alteration by some external means of introducing heat. The second law states that changes in the sum of the Entropy of a system and its surroundings must constantly be positive to progress towards thermodynamic equilibrium with a specific absolute supreme value of Entropy.
The generality of the second law provides a powerful means to comprehend the thermodynamic aspects of natural systems by utilizing ideal systems. Kelvin-Planck stated that a system could not receive a certain amount of heat from a high-temperature reservoir and deliver equivalent work productivity. Hence, achieving a heat engine whose thermal efficiency is 100 %( Dincer & Cengel, 2001) is difficult. Clausius cited the impossibility of a system to transmit heat from a lower temperature reservoir to a higher one since heat transmission can only spontaneously happen in the direction of temperature decrease.
Conclusion
A dependable theoretical basis for temperature was established when Clausius defined the equivalent of Entropy, defining a unique thermodynamic temperature. Entropy is more fundamental compared to the more available temperature. According to the second law of thermodynamics, all energy transfers or conversions are irreversible and spontaneously happen toward increasing Entropy. As a result, some of the losses in a power plant can only be minimized, but none of them can be eradicated. The usual approach is to convert some low-entropy energy by friction or electrical resistance. The third law of thermodynamics quantifies the period taken to cool a system. Therefore as the second law presents that thermodynamic transitions are possible, the third law enumerates the time of such transitions. In this context, searching the time and resource costs of other transitions is interesting while exploring the third law in additionally restricted physical surroundings.
References
Brandao, F., Horodecki, M., Ng, N., Oppenheim, J., & Wehner, S. (2015). The second law of quantum thermodynamics. Proceedings of the National Academy of Sciences, 112(11), 3275-3279.
Connor N. (2019, May 22). What is Entropy – Definition. Thermal Engineering. https://www.thermal-engineering.org/what-is-entropy-definition/
Dincer, I., & Cengel, Y. A. (2001). Energy, entropy and exergy concepts and their roles in thermal engineering. Entropy, 3(3), 116-149.
Elliott, J. R., Lira, C. T., & Lira, C. T. (2012). Introductory chemical engineering thermodynamics (Vol. 668). Upper Saddle River, NJ: Prentice Hall.
Fairen, V., Hatlee, M., & Ross, J. (1982). Thermodynamic processes, time scales, and entropy production. The Journal of Physical Chemistry, 86(1), 70-73.
Jensen, W. B. (2004). Entropy and Constraint of Motion. Journal of Chemical Education, 81(5), 639.
Lambert, F. L. (2002). Disorder-A cracked crutch for supporting entropy discussions. Journal of Chemical Education, 79(2), 187.
 write
write