Introduction
Refrigerators are one of the most important household items in the cooling equipment category. The basic design of a refrigerator comprises a thermally insulated compartment in conjunction with a proper mechanism to lower the temperature inside the refrigerator. The compartment also ensures that the heat inside the refrigerator is transferred to the external environment. This keeps the food items at a lower temperature and prevents spoilage, which could have happened at room temperature. In the market today, refrigerators come in different sizes.
For the refrigerator, thermal loads translate to the amount of heat that needs to be removed to maintain a lower temperature. These thermal loads for a refrigerator depend on the refrigerator’s size, the ambient room temperature, the duration and frequencies of door openings and the insulation of the refrigerator. Therefore in the design of a kitchen refrigerator, one has to estimate the thermal loads based on the following factors discussed above. Some of the basic steps during design include the determination of the refrigerator size, calculation of the thermal load, selection of a refrigeration system, selection of insulation, design of a compressor, design of a condenser and evaporator, as well as optimization of the whole system.
Therefore, this report aims to analyze thermal loads and partially design a typical kitchen refrigerator. The thermal loads include the heat transfer through the loads, the energy extracted from the products and the door-opening effects. The report also contains main conclusions and recommendations for future work.
1. Part 1: Thermal loads
This section provides the cooling load required for the refrigerator in (kW). This is the rate of energy that must be removed from the compartment of the refrigerator so that the products are maintained at a desired temperature. For this to succeed, we consider three important things; The heat transfer through the walls, the energy extracted from the products and the door-opening effects.
1.1 Degrees of Freedom
- Temperature inside the refrigerator =3°C
- Isentropic efficiency of the compressor = 0.90
- Temperature of the Kitchen = 25°C
- Chosen cooling time = 1,200 seconds
1.2 Heat transfer through the walls of a refrigerator
The air in the kitchen has a higher temperature than the refrigerator’s interior. The temperature inside the refrigerator and the one in the kitchen are not in equilibrium; thus, heat will be transferred from the kitchen into the fridge based on the second law of thermodynamics. For this case, we consider a freezerless refrigerator with dimensions of 0.762×0.784×1.674 as the width, depth and height, respectively;
The total surface area will be given by
S.A=(0.784×0.762) x2) + (1.674×0.784)x2)+(1.674×0.762)x2) = 1.19+2.62+2.55=6.36m2
The rate of heat transfer will be given by
Qwalls = 0.004.A.(Tkit – Tin)
= 0.004×6.36M2(25°C-3°C)
=0.02544M2(22°C)
=5.57kW .
1.3 Energy to be extracted from products
The table below shows the list of items that will be restocked into the refrigerator. The table also indicates various foodstuff heat capacities (Engineering ToolBox, 2023).
Table 1: List of food items to be restocked
| Item | Quantity(Kgs) | Room temperature(°C) | Specific heat capacity (c)kJ/(kg°C) | ∆T(°C) | Q = (m*c*∆T)/1000 in kJ | E = QxCOP in kJ |
| Apples | 1kg | 25 | 3.64 | 22 | 0.08 | 0.072 |
| Beef, rib | 2kg | 25 | 2.81 | 22 | 0.12 | 0.108 |
| Cabbage | 0.5 | 25 | 3.94 | 22 | 0.04 | 0.036 |
| Chicken Broiler | 4kg | 25 | 3.22 | 22 | 0.283 | 0.254 |
| Kale | 2kg | 25 | 3.73 | 22 | 0.16 | 0.144 |
| Milk, cow – whole pasteurized | 2kg | 25 | 3.77 | 22 | 0.16 | 0.144 |
| Total | 0.758 |
The amount of energy that will be needed to cool down the above items can be calculated using the following formula
Q=m*c*∆T
Where
Q = amount of heat energy that needs to be removed (in joules)
m = is the mass of the items (in kilograms)
c = is the specific heat capacity of the item (in joules per kg per degree Celsius)
∆T = Temperature difference between the initial and the desired temperature.
The amount of heat energy that needs to be extracted from the item in order to cool it down is given by
E= QxCOP
Where
E = amount of energy that is supposed to be extracted
COP = Coefficient of performance of the cooling system that is being used
The following formulae will give the cooling power required
P= Q/t
Where
P = is the cooling power( watts)
Q = is the total energy required (Joules)
t = is the time of Cooling (seconds)
The total energy in joules will be given by
Q = (0.072+0.108+0.036+0.254+0.144+0.144)kJ
=758J
P = 758J/ 1200s
P = 0.00063kW.
1.4 Door Opening Effects
In order to find the volume of air inside the refrigerator, the dimensions of the refrigerator have to be known. For the freezeless refrigerator considered in this case
Volume = length x height x width
= 1.674 x 0.784×0.762
= 1.0 m3
At STP conditions density of air is 1.225kg/m3
The mass of air in the fridge will be given by density x volume
Mass = 1.225kg/m3 x 1.0m3
Mass =1.225kg
Power required to cool down the air that leaks into the fridge can also be found. When the door opens, 20% of the air in the fridge is replaced with hot kitchen air. The mass of kitchen air that leaks into the fridge when the door is opened is given by
Mass of kitchen air = 20% x mass of air in the fridge
Mass of kitchen air = 0.2×1.225kg
Mass of kitchen air = 0.245kg
We must cool the hot kitchen air from 25°C to 3°C inside the fridge. The amount of heat that needs to be removed can be calculated using Q = m x c x △T. Or this case; the temperature difference is 22°C. The specific heat capacity (c) of air is 1.005 kJ/(kg·K). Therefore
Q = 0.245kg x 1.005 kJ/(kg·K).x22°C
Q = 5.4kJ.
If the frequency of opening the door is once every 60 minutes, then the power required to cool down the air that leaks into the fridge is given by;
P = Q/t
P = 5.4kJ/3600s
P = 0.0015kW.
The power required to cool down the air that leaks into the fridge is very small; however, if the frequency of opening the fridge is increased, the power required to cool down the air leaks will also increase.
2. Part 2 – Calculations
This part shows the calculations that were done to inform the analysis
2.1 Cooling load (CL) in kW as explained in part 1.
Solution
CL = (0.0015 + 0.00063 + 5.57)kW
= 5.7213kW .
2.2 The mass flow rate of refrigerant R-134a in kg/s.
Solution
This refrigeration system operates with R-134a as the working fluid. The cooling load is 5.7213kW. The condenser pressure is 850kPa (8.5 bar), and the evaporator pressure is 180kPa (1.8 bar). The refrigerant enters the compressor at -9°C and leaves the condenser at 30°C.
The mass flow rate will then be given by
Mass flow rate = Cooling capacity of the fridge ( Density of refrigerant x enthalpy difference).
The enthalpy values for R-134a at the specified temperatures and values are 322.87 and 286.4 kJ/kg (Engineering ToolBox).
Enthalpy difference is thus = 322.87 -286.4 = 36.47 kJ/kg
The refrigerant density at the condenser for R-134a at 8.5 bar and 30°C is approximately 0.888 kg/m3.
Hence the mass flow rate = 5.7213kW/ (36.47 kJ/kg x 0.888 kg/m3)
Mass flow rate = 0.177 kg/s
2.3The electrical work consumed by the compressor in kW
Solution
Using a compressor with a power rating of 7.45 kW, an efficiency of 0.9 works for 10 hours a day where the voltage supplied to the compressor is 240 V and the current drawn is 30A.
Then electrical work (kW) = (Power rating efficiency)/Power factor
= (7.45 x 0.9)/1
= 6.75kW.
Total electrical work(kWh) = 6.75x 10 = 67.5kWh.
2.4 The rate of heat dissipated by the condenser in kW
Solution
The cooling capacity is 5.7213kW. The temperature entering the condenser is -9°C, and the leaving temperature is 30°C. The mass flow rate of the refrigerant is 0.177 kg/s. The heat dissipated by the condenser is thus given by
Q = m * (h1 – h2)
Where
Q = is the rate of heat dissipated
m = is the mass flow rate of the refrigerant
h1-h2 = is the enthalpy difference between the inlet and outlet.
For our case, the enthalpy difference is 36.47 kJ/kg
Hence the rate of heat dissipated by the condenser can be given by
Q = 0.177 kg/s x 36.47 kJ/kg
= 6.45kW .
2.5 The Coefficient of performance of your refrigerator.
Solution
Amount of heat removed (dissipated) = 6.45x 1000 =6450W
Total amount of electrical work = 67.5 /10 = 6.75kW x1000 = 6750W
We know that 1 watt = 1 joule/second
COP = Heat removed from the refrigerator/ electrical work put in the refrigerator
= 6450 Js/6750J/s
= 0.95.
This means that for one unit of electrical energy supplied to the refrigerator, 0.95 units of heat are removed from its compartments.
2.6 The temperature – entropy (T-s) diagram of the cycle clearly showing the 4 points labelled in Figure 2
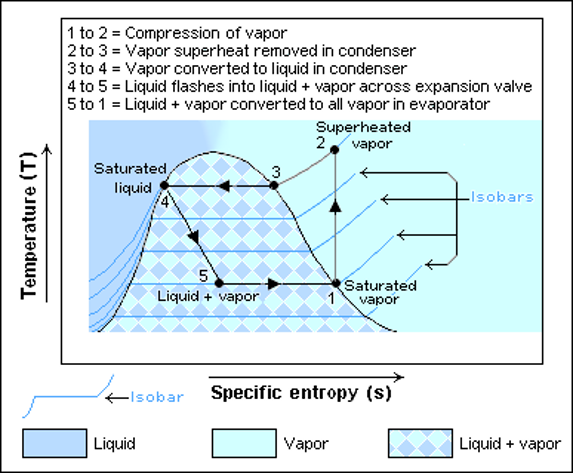
The refrigeration cycle begins at point 1 when the refrigerant is gaseous. At this point, there is high temperature and high entropy. The refrigerant is compressed to very high pressure, and the temperature rises to point 2. The refrigerant then enters the condenser, releasing heat to the surrounding environment; the temperature then drops to points 3 and 4. The refrigerant then goes through the expansion valve, and through a throttling process, its temperature is lowered to point 4. The refrigerant then enters the evaporator, where it gains heat from the surroundings, and then its temperature increases to point 1 and the refrigeration cycle is completed. The T-S diagram indicates the work done by the refrigerator in every single cycle.
Conclusion
A kitchen refrigerator has been partially designed after analysis of the thermal loads. The thermal loads have been determined, the Qwalls are 5.57kW, and after restocking, the energy to be extracted is 758J, and the door opening effects have been found to pose an extra demand of 0.0015kW. A typical kitchen refrigerator with 0.95 as a coefficient of performance has been partially designed. The goals of this report have been fully achieved. In the future, I would like to add a freezer to the refrigerator to have two compartments. Careful analysis will ensure proper design.
References
Engineering Toolbox. (2023). Food and foodstuff – specific heat. Engineering Toolbox. Retrieved April 20, 2023, from https://www.engineeringtoolbox.com/specific-heat-capacity-food-d_295.html
Engineering Toolbox. (n.d.). Refrigerant r134a – properties. Engineering Toolbox. Retrieved April 20, 2023, from https://www.engineeringtoolbox.com/r134a-properties-d_1682.html
Mechneer, T. R. (2013, September 18). Refrigeration and methods of refrigeration. Urmish creative solutions. Retrieved April 20, 2023, from https://theroyalmechneers.wordpress.com/2013/09/18/refrigeration-and-methods-of-refrigeration/
 write
write